
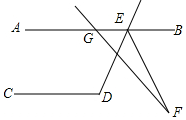
 如图,AB∥CD,∠CDE=116°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=8°.
如图,AB∥CD,∠CDE=116°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=8°. 分析 先根据平行线的性质求出∠AED与∠DEB的度数,再由角平分线的性质求出∠DEF的度数,进而可得出∠GEF的度数,再根据三角形外角的性质即可得出结论.
解答 解:∵AB∥CD,∠CDE=116°,
∴∠AED=180°-116°=64°,∠DEB=116°.
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=$\frac{1}{2}$×116°=58°,
∴∠GEF=64°+58°=122°.
∵∠AGF=130°,
∴∠F=∠AGF-∠GEF=130°-122°=8°.
故答案为:8°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补;两直线平行,内错角相等.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
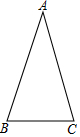 如图,在△ABC中,AB=AC,∠ABC=70°.
如图,在△ABC中,AB=AC,∠ABC=70°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | 0 | 1 | 2 | … |
| y | … | 7 | -1 | -2 | -1 | … |
| A. | 抛物线开口向下 | B. | 抛物线的对称轴是y轴 | ||
| C. | x<1时,y随x的增大而减小 | D. | 抛物线与y轴交于正半轴 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{\frac{5}{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com