
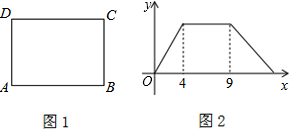
如图(1)所示,在矩形ABCD中,AB=20cm,DC=4cm,点P从A开始沿折线A—B—C—D以4cm/s的速度移动,点Q从C开始沿CD边以1cm/s的速度移动,如果P,Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动.设运动时间为t(s).
(1)t为何值时,四边形APQD为矩形?
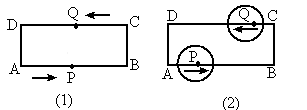
(2)如图6(2)所示,如果⊙P和⊙Q的半径都是2cm,那么t为何值时,
⊙P和⊙Q外切?
|
解: (1)由题意知,当AP=DQ,AP∥DQ,∠A=90°时,四边形APQD为矩形,此时4t=20-t,∴t=4(s),∴t为4s时,四边形APQD为矩形. (2)当PQ=4时,⊙P与⊙Q外切.①如果点P在AB上运动,只有当四边形APQD为矩形时,PQ=4,由(1)得t=4s②如果点P在BC上运动,此时t≥5,则CQ≥5,PQ≥CQ≥5>4,∴⊙P与⊙Q外离.③如果点P在CD上运动,且点P在点Q的右侧,可得CQ=t,CP=4t-24.当CQ-CP=4时,⊙P与⊙Q外切,此时t-(4t-24)=4,∴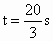 .④如果点P在CD上运动,且点P在点Q的左侧,当CP-CQ=4时,⊙P与⊙Q外切.此时4t-24-t=4,∴ .④如果点P在CD上运动,且点P在点Q的左侧,当CP-CQ=4时,⊙P与⊙Q外切.此时4t-24-t=4,∴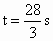 .∵点P从A开始沿折线A?/FONT>B?/FONT>C?/FONT>D移动到D需要11s,点Q从C开始沿CD边移动到D需要20s,而 .∵点P从A开始沿折线A?/FONT>B?/FONT>C?/FONT>D移动到D需要11s,点Q从C开始沿CD边移动到D需要20s,而 ,∴当t为4s, ,∴当t为4s, , ,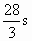 ,⊙P叫⊙Q外切. ,⊙P叫⊙Q外切. |


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、10 | B、16 | C、18 | D、32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 |
| 5 |
| 4 |
| 3 |
| 8 |
| 5 |
| 4 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com