
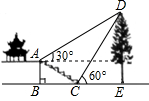
 某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)
某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号) 分析 首先表示出AF的长,进而得出BC的长,再表示出CE=$\frac{\sqrt{3}}{3}$(x+2),利用EB=BC+CE求出答案.
解答 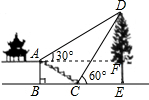 解:过点A作AF⊥DE,设DF=x,
解:过点A作AF⊥DE,设DF=x,
在Rt△ADF中,∵∠DAF=30°,tan∠DAF=$\frac{DF}{AF}$=$\frac{\sqrt{3}}{3}$,
∴AF=$\sqrt{3}$x,
AC的坡度i=1:2,
∴$\frac{AB}{CB}$=$\frac{1}{2}$,
∵AB=2,
∴BC=4,
∵AB⊥BC,DE⊥CE,AF⊥DE,
∴四边形ABEF为矩形,
∴EF=AB=2,BE=AF,
∴DE=DF+EF=x+2,
在Rt△DCE中,tan∠DCE=$\frac{DE}{CE}$,
∵∠DCE=60°,
∴CE=$\frac{\sqrt{3}}{3}$(x+2),
∵EB=BC+CE=4+$\frac{\sqrt{3}}{3}$(x+2),
∴$\frac{\sqrt{3}}{3}$(x+2)+4=$\sqrt{3}$x,
∴x=1+2$\sqrt{3}$,
∴DE=3+2$\sqrt{3}$.
点评 此题主要考查了解直角三角形的应用,以及矩形的判定和性质,三角函数,借助仰角构造直角三角形并解直角三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
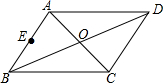 已知,如图平行四边形ABCD中,对角线AC、BD交于点O,点E是AB边上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),那么$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量吗?为什么?
已知,如图平行四边形ABCD中,对角线AC、BD交于点O,点E是AB边上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),那么$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com