
【题目】某市为解决农村燃气困难,在P处建立了一个燃气站,从P站分别向A、B、C村铺设燃气管道。已知B村在A村的北偏东60°方向,距离A村2.4km,C村在A村的正东方向,距离A村1.8km,要使此工程费用最省,管道PA+PB+PC之和需最短,则最短长度为______________km.

【答案】3
【解析】
先证明△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.然后根据这个原理找到点P,把△APC绕点A逆时针旋转60°得△ADE,证得△ABE是直角三角形,用勾股定理求出BE,即可得出PA+PB+PC之和的最短值。
解:先证明结论:△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
如图1, P为△ABC内一点,∠APB=∠BPC=120°,
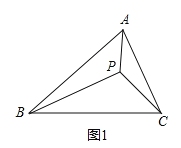
证明:如图2,将△ACP绕点A逆时针旋转60°得到△ADE,

∴∠PAD=60°,△PAC≌△DAE,
∴PA=DA、PC=DE、∠APC=∠ADE=120°,
∴△APD为等边三角形,
∴PA=PD,∠APD=∠ADP=60°,
∴∠APB+∠APD=120°+60°=180°,∠ADP+∠ADE=180°,即B、P、D、E四点共线,
∴PA+PB+PC=PD+PB+DE=BE.
∴PA+PB+PC的值最小.
解决问题:
如图3,将三个村连接为△ABC,由上可知,当∠APB=∠APC=∠BPC=120°时,AP+BP+PC的值最小.
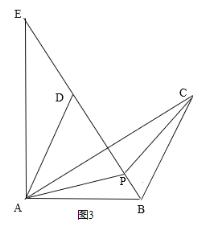
把△APC绕点A逆时针旋转60°得△ADE,
∴∠PAD=60°,AE=AC=2.4 km
由上可知B、P、D、E共线,且AP+BP+PC=BE,∠PAB=∠DAE,
∵B村在A村的北偏东60°方向, C村在A村的正东方向,
∴∠BAC=30°,
∴∠PAB+∠PAC=∠DAE+∠PAB=30°,
∴∠BAE=∠DAE+∠PAB+∠PAD=90°,
在Rt△ABE中,
![]()
∴PA+PB+PC=3km
故答案为:3


科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
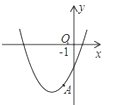
A. b2>4ac B. m>n C. 方程ax2+bx+c=﹣4的两根为﹣5或﹣1 D. ax2+bx+c≥﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
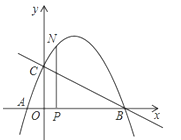
【题目】如图,抛物线与x轴交于点A(﹣![]() , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣![]() <t<2),求△ABN的面积s与t的函数解析式;
<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
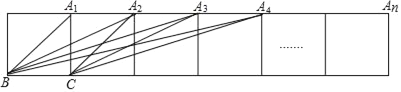
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A.B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=kx-1上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=kx-1上,则a的值是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
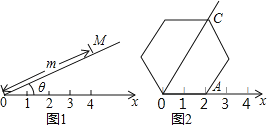
A.(60°,4) B.(45°,4) C.(60°,2![]() ) D.(50°,2
) D.(50°,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0)、C(0,﹣3).
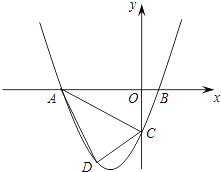
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?如存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com