
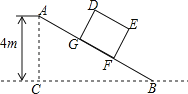
【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(结果保留根号)
【答案】(1)BC=8m;(2)2![]() m.
m.
【解析】
(1)根据坡度定义直接解答即可;
(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据![]() ,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
解:(1)∵坡度为i=1∶2,AC=4m,
∴BC=4×2=8m.
(2)作DS⊥BC,垂足为S,且与AB相交于H.
∵∠DGH=∠BSH,∠DHG=∠BHS,
∴∠GDH=∠SBH,
∴![]() ,
,
∵矩形DEFG为长方体
∴DG=EF=2m,
∴GH=1m,
∴DH=![]() m,BH=BF+FH=3.5+(2.5﹣1)=5m,
m,BH=BF+FH=3.5+(2.5﹣1)=5m,
设HS=xm,则BS=2xm,
∴x+(2x)=5,
∴x=![]() m
m
∴DS=![]() +
+![]() =
=![]() m.
m.


科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
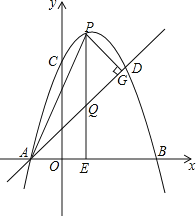
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.
(1)求抛物线的解析式;
(2)求点D的坐标及直线AD的解析式;
(3)当点P在直线AD上方时,求d关于m的函数关系式,并求出d的最大值;
(4)当点P在直线AD上方时,若PQ将△APG分成面积相等的两部分,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
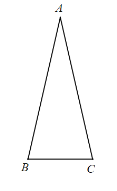
【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是_____.
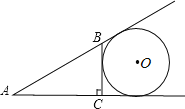
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
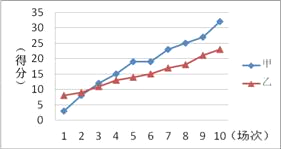
A. 甲运动员得分的平均数小于乙运动员得分的平均数B. 甲运动员得分的中位数小于乙运动员得分的中位数
C. 甲运动员得分的最小值大于乙运动员得分的最小值D. 甲运动员得分的方差大于乙运动员得分的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
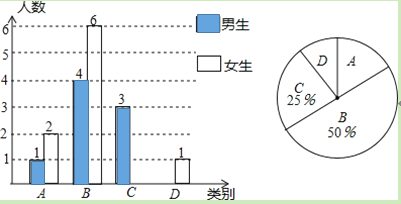
(1)本次调查中C类女生有______名,D类男生有______名;将上面的条形统计图补充完整;
(2)计算扇形统计图中D所占的圆心角是______;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为弓形AB的弦,AB=2![]() ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
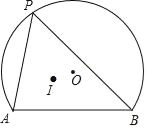
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com