
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F. 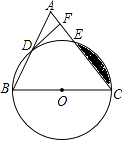
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为20,cosB= ![]() ,求阴影部分面积.
,求阴影部分面积.
【答案】
(1)证明:如图1,连接CD,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴点D是AB的中点
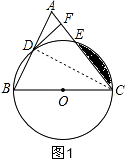
(2)解:DF与⊙O相切,如图2,连接OD,
∵O是BC的中点,点D是AB的中点,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF与⊙O相切
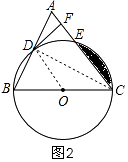
(3)证明:如图3,连接OE、BE,
∵cos∠ABC= ![]() ,
,
∴∠ABC=60°,
∵AC=BC,
∴△ABC是等边三角形,
∴∠ECB=60°,
∵BC是⊙O的直径,
∴∠BEC=90°,
∴∠EBC=30°,
∴∠EOC=60°,
∵BC=20,
∴EC=10,
由勾股定理得:BE= ![]() =10
=10 ![]() ,
,
∴S△OEC= ![]() S△BEC=
S△BEC= ![]() ×
× ![]() BECE=
BECE= ![]() ×10
×10 ![]() ×10=25
×10=25 ![]() ,
,
∴S阴影=S扇形OEC﹣S△OEC= ![]() ﹣25
﹣25 ![]() =
= ![]() ﹣25
﹣25 ![]() .
.
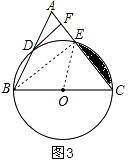
【解析】(1)连接CD,根据直径所对的圆周角为90°得∠BDC=90°,再由等腰三角形的三线合一得出结论;(2)根据中位线的定义可以知道:OD是△ABC的中位线,则OD∥AC,因为DF⊥AC,所以DF⊥OD,得出DF与⊙O相切;(3)如图3,连接OE、BE,先根据特殊的三角函数值求出∠ABC=60°,所以△ABC是等边三角形,求出直角△BEC各边的长,就可以求其面积,根据中线的性质可知△OEC的面积就是△BEC面积的﹣半,所求的阴影面积是扇形面积与△OEC的面积的差.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.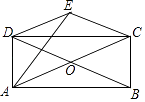
(1)求证:四边形OCED是菱形;
(2)连接AE,若AB=6cm,BC= ![]() cm.
cm.
①求sin∠EAD的值;
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC. 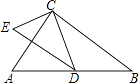
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C为直角,AC=5,BC=12,在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放个. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( ) 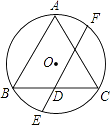
A.![]() +1
+1
B.2 ![]() ﹣2
﹣2
C.2 ![]() ﹣2
﹣2
D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张正方形纸板的边长为2cm,将它剪去4个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=xcm,四边形EFGH的面积为ycm2 , 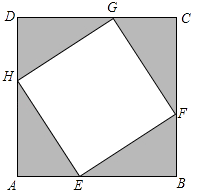
(1)求y关于x的函数表达式和自变量x的取值范围;
(2)求四边形EFGH的面积为3cm2时的x值;
(3)四边形EFGH的面积可以为1.5cm2吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2017年中考,某中学对全校九年级学生进行了一次数学期末模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题: 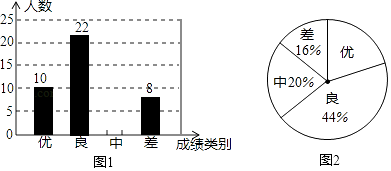
(1)在这次调查中,样本中表示成绩类别为“中”的人数;
(2)将条形统计图补充完整;
(3)若该中学九年级共有800人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: 
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com