
【题目】已知反比例函数的图![]() 象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
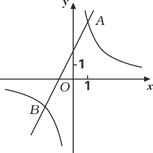
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
【答案】(1)![]() ,y2=2x+2.(2)x<﹣2 或0<x<1.
,y2=2x+2.(2)x<﹣2 或0<x<1.
【解析】试题分析:(1)将点A坐标代入y1=![]() 中,得以k的值,即可得到反比例函数的解析式,将点B坐标代入反比比例函数的解析式中即可求出m的值,再将A、B两点坐标代入y2=ax+b中,从而求出a、b的值,即为一次函数的解析式;
中,得以k的值,即可得到反比例函数的解析式,将点B坐标代入反比比例函数的解析式中即可求出m的值,再将A、B两点坐标代入y2=ax+b中,从而求出a、b的值,即为一次函数的解析式;
(2)由y1>y2,即写出反比例函数图像在一次函数图像上方时对应自变量x的取值范围即可;
试题解析:
(1)∵函数y1=![]() 的图象过点A(1,4),即k=4,
的图象过点A(1,4),即k=4,
∴k=4,即y1=4/x,
又∵点B(m,﹣2)在y1上,
∴m=﹣2,∴B(﹣2,﹣2),
又∵一次函数y2=ax+b过A、B两点,
即 ![]() ,解之得
,解之得![]() .
.
∴y2=2x+2.
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴x<﹣2 或0<x<1.


科目:初中数学 来源: 题型:
【题目】在一个口袋里有四个完全相同的小球,把它们分别标号为1,2,3,4,小明和小强采取的摸取方法分别是:
小明:随机摸取一个小球记下标号,然后放回,再随机摸取一个小球,记下标号;
小强:随机摸取一个小球记下标号,不放回,再随机摸取一个小球,记下标号.
(1)用画树状图(或列表法)分别表示小明和小强摸球的所有可能出现的结果;
(2)分别求出小明和小强两次摸球的标号之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com