
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.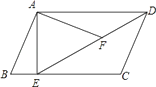
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD= ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC
(2)解:∵CD=AB=4,AE⊥BC,
∴AE⊥AD; 在Rt△ADE中,DE= ![]() ,
,
∵△ADF∽△DEC,
∴ ![]() ;
;
∴ ![]() ,
,
解得AF= ![]()
【解析】(1)根据平行四边形的性质证出AD∥BC,AB∥CD,结合已知∠AFE=∠B.得出∠ADF=∠CED,∠AFD=∠C再根据两组角对应相等的两个三角形相似证得结论。
(2)根据平行四边形的性质及已知AE⊥BC,证明△ADE是直角三角形,利用勾股定理求出DE的长,再根据相似三角形的性质(△ADF∽△DEC)。得对应线段成比例,建立方程求出AF的长。


科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为 ![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D.“抛一枚正方体骰子,朝上的点数为2的概率为 ![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 ![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“拼图,推演,得到了整式的乘法的法则和乘法公式.教材第9章头像拼图这样,借助图形往往能把复杂的数学问题变得简明、形象.
(分数运算)
怎样理解![]() ?
?

从图形的变化过程可以看出,长方形先被平均分成3份,取其中的2份(涂![]() 部分);再将涂色部分平均分成5份,取其中4份(涂
部分);再将涂色部分平均分成5份,取其中4份(涂![]() 部分).这样,可看成原长方形被平均分成15份,取出其中8份,所以
部分).这样,可看成原长方形被平均分成15份,取出其中8份,所以![]() 的
的![]() 占原长方形的
占原长方形的![]() ,即
,即![]() .
.
(尝试推广)
(1)①类比分数运算,猜想![]() 的结果是____________;(a、b、c、d均为正整数,且
的结果是____________;(a、b、c、d均为正整数,且![]() ,
,![]() );
);
②请用示意图验证①的猜想并用文字简单解释.
(2)①观察下图,填空:![]() ____________;
____________;

②若a、b均为正整数且![]() ,猜想
,猜想![]() 的运算结果,并用示意图验证你的猜想,同时加以简单的文字解释.
的运算结果,并用示意图验证你的猜想,同时加以简单的文字解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com