
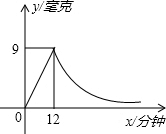
 近来,禽流感又在抬头,已经夺去近10人的生命,病症与“非典”极为相似,为了同学们的身心健康,学校在休息日用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放过程中,y与x成反比例.如图所示,根据题中提供的信息,解答下列问题:
近来,禽流感又在抬头,已经夺去近10人的生命,病症与“非典”极为相似,为了同学们的身心健康,学校在休息日用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放过程中,y与x成反比例.如图所示,根据题中提供的信息,解答下列问题:分析 (1)药物燃烧时,设出y与x之间的解析式y=k1x,把点(12,9)代入即可,从图上读出x的取值范围;药物燃烧后,设出y与x之间的解析式y=$\frac{{k}_{2}}{x}$,把点(12,9)代入即可;
(2)把y=0.45代入反比例函数解析式,求出相应的x的值即可.
解答 解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(12,9)为9=12k1,
解得k1=$\frac{3}{4}$,
设药物燃烧后y关于x的函数关系式为y=$\frac{{k}_{2}}{x}$(k2>0),
代入(12,9)为9=$\frac{{k}_{2}}{12}$,
解得k2=108.
所以药物燃烧时y关于x的函数关系式为y=$\frac{3}{4}$x(0≤x≤9),药物燃烧后y关于x的函数关系式为y=$\frac{108}{x}$(x>9);
(2)结合实际,令y=$\frac{108}{x}$中,y≤0.45,解得x≥240.
即从药物燃烧开始,至少需要经过240分钟后,学生才能进入教室.
点评 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c的图象与x轴交于点(-3,0),(x1,0),且2<x1<3,与y轴的负半轴交于点(0,-3)的上方.下列结论:①a>b>0;②6a+c<0;③9a+c>0;④3a<b+1.其中正确结论的个数为( )
已知二次函数y=ax2+bx+c的图象与x轴交于点(-3,0),(x1,0),且2<x1<3,与y轴的负半轴交于点(0,-3)的上方.下列结论:①a>b>0;②6a+c<0;③9a+c>0;④3a<b+1.其中正确结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{(a-1)^{2}}$ | B. | a-1 | C. | $\frac{1}{a}$ | D. | $\frac{a-1}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 计算:在直角坐标系中,标出下列各点的位置,并写出各点的坐标.
计算:在直角坐标系中,标出下列各点的位置,并写出各点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直径是经过圆心的弦 | |
| B. | 半径相等的两个半圆是等弧 | |
| C. | 三角形的内心到三角形各顶点的距离相等 | |
| D. | 经过不共线三点必作一个圆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com