
【题目】如图,在边长为5的正方形ABCD中,点E在BC边上,连接AE,过D作DF//AE交BC的延长线于点F,过点C作CG⊥DF于点G,延长AE、GC交于点H,点P是线段DG上的任意一点(不与点D、点G重合),连接CP,将△CPG沿CP翻折得到![]() ,连接
,连接![]() . 若CH=1,则
. 若CH=1,则![]() 长度的最小值为__________.
长度的最小值为__________.

【答案】![]()
【解析】
如图,作DM⊥AE于M,首先证明四边形DMHG是正方形,求出正方形DMHG的边长,以及AC的长,因为点P在线段DG上运动时,点G′在以C为圆心,CG为半径的圆上运动,所以当A、G′、C共线时,AG′最小.由此即可解决问题.
解:如图,作DM⊥AE于M.设CG=x,
∵AH∥DF,GH⊥DF,
∴∠MHG=∠HGD=∠DMH=90°,
∴四边形DMHG是矩形,
∵∠ADC=∠MDG=90°,
∴∠ADM=∠CDG,
在△ADM和△CDG中,
 ,
,
∴△ADM≌△CDG(AAS),
∴DM=DG,
∴四边形DMHG是正方形,
∴GH=DG,
∵CH=1,CG=x,
∴DG=CG+HC=x+1,
在Rt△DCG中,![]() ,
,
∴x=3,x=-4(舍去),
∴CG′=CG=3,
在Rt△ADC中,AC= ![]() ,
,
∵点P在线段DG上运动时,点G′在以C为圆心,CG为半径的圆上运动,
∴当A、G′、C共线时,AG′最小,
∴AG′的最小值为AC-CG′= ![]() .
.
故答案为:![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】武汉市政府大力扶持大学生创业,童威在政府的扶持下投资销售一种进价为每盏20元的护眼台灯,销售过程中发现,每月销售量y(盏)与销售单价x(元)之间的关系可近似地看作一次函数:y=﹣10x+500.
(1)设每月获得的利润为w(元),求w与x的关系式.
(2)如果想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元.如果童威想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为P,且与y轴交于点A,与直线
的顶点为P,且与y轴交于点A,与直线![]() 交于点B,C(点B在点C的左侧).
交于点B,C(点B在点C的左侧).

(1)求抛物线![]() 的顶点P的坐标(用含a的代数式表示);
的顶点P的坐标(用含a的代数式表示);
(2)横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.
①当![]() 时,请直接写出“W区域”内的整点个数;
时,请直接写出“W区域”内的整点个数;
②当“W区域”内恰有2个整点时,结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
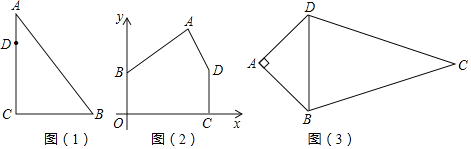
【题目】(1)问题提出:如图(1),在直角△ABC中,∠C=90°,AC=8,BC=6,点D为AC上一点且AD=2,过点D作直线DE交△ABC于点E,使得△ABC被分成面积相等的两部分,则DE的长为 .
(2)类比发现:如图(2),五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C(4,0),D(4,2)请你找出一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,求出该直线对应的函数表达式.
(3)如图(3),王叔叔家有一块四边形菜地ABCD,他打算过D点修一条笔直的小路把四边形菜地ABCD分成面积相等的两部分,分别种植不同的农作物,已知AB=AD=200米,BC=DC=200![]() 米,∠BAD=90°过点D是否存在一条直线将四边形ABCD的面积平分?若存在,求出平分该四边形面积的线段长:若不存在,请说明理由.
米,∠BAD=90°过点D是否存在一条直线将四边形ABCD的面积平分?若存在,求出平分该四边形面积的线段长:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.

(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,∠AOB=90°,OA=4,OB=3,点E在线段OA上,EP⊥OA交AB于点N,PM⊥AB,直线PB与AO交于点F.
(1)若AN=3,S△PBN=8,求PN的长;
(2)设△PMN的周长为C1,△AEN的周长为C2,若△PFE~△BAO且![]() =
=![]() ,求OE的长;
,求OE的长;
(3)如图2,若OE=2,将线段OE绕点O逆时针旋转得到OE',旋转角为α (0°<α<90°),连接E'A、E'B,求E'A+![]() E'B的最小值.
E'B的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个三等分数字转盘,小红先转动转盘,指针指向的数字记下为![]() ,小芳后转动转盘,指针指向的数字记下为
,小芳后转动转盘,指针指向的数字记下为![]() ,从而确定了点
,从而确定了点![]() 的坐标
的坐标![]() ,(若指针指向分界线,则重新转动转盘,直到指针指向数字为止)
,(若指针指向分界线,则重新转动转盘,直到指针指向数字为止)
(1)小红转动转盘,求指针指向的数字2的概率;
(2)请用列举法表示出由![]() ,
,![]() 确定的点
确定的点![]() 所有可能的结果.
所有可能的结果.
(3)求点![]() 在函数
在函数![]() 图象上的概率.
图象上的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
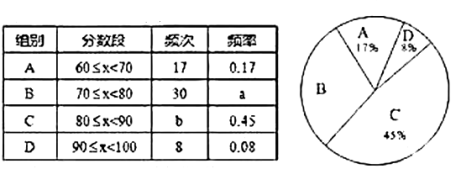
【题目】为了传承中华优秀的传统文化,市教育局决定开展“经典诵读进校园”活动,某校园团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表:
请根据所给信息,解答以下问题:
(1)表中![]() ;
;![]() ;
;
(2)请计算扇形统计图中![]() 组对应的圆心角的度数;
组对应的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列举法或树状图法求甲、乙两名同学都被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com