
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
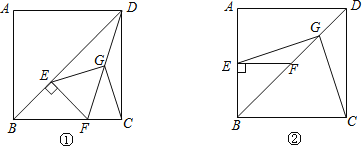
(1)求证:EG=CG;EG⊥CG.
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)结论仍然成立,证明见解析
【解析】
试题分析:(1)根据直角三角形斜边中线的性质以及三角形外角定理即可证明.
(2)作GM⊥BC于M,⊥AB于N交CD于H,只要证明△GNE≌△GMC即可解决问题.
证明:(1)如图①中,∵四边形ABCD是正方形,
∴∠BCD=∠ADC=90°,∠BDC=![]() ,
,
∵EF⊥BD,
∴∠DEF=90°,
∵GF=GD,
∴EG=DG=GF=![]() DF,GC=DG=GF=
DF,GC=DG=GF=![]() DF,
DF,
∴EG=GC,∠GED=∠GDE,∠GCD=∠GDC,
∵∠EGF=∠GED+∠GDE=2∠EDG,∠CGF=∠GCD+∠GDC=2∠GDC,
∴∠EGC=∠EGF+∠CGF=2∠EDG+2∠GDC=2(∠EDG+∠GDC)=90°,
∴EG⊥GC.
(2)图②中,结论仍然成立.
理由:作GM⊥BC于M,⊥AB于N交CD于H.
∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,∠ABD=∠DBC=∠BDC=45°
∴GM=GN,
∵∠A=∠ANG=∠ADH=90°,
∴四边形ANHD是矩形,
∴∠DHN=90°,∠GDH=∠HGD=45°,
∴HG=DH=AN,同理GH=CM,
∵∠ENG=∠A=∠BEF=90°,
∴EF∥GN∥AD,∵GF=GD,
∴AN=NE=GH=MC,
在△GNE和△GMC中,
 ,
,
∴△GNE≌△GMC,
∴GE=GC,∠NGE=∠MGC,
∴∠EGC=∠NGM=90°,
∴EG⊥GC.



科目:初中数学 来源: 题型:
【题目】把a42a2b2+b4分解因式,结果是( )
A. a2(a22b2)+b4 B. (a2b2)2 C. (ab)4 D. (a+b)2(ab)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
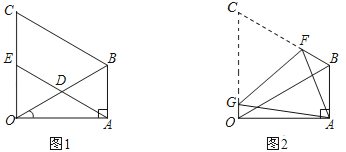
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人在运动时每分钟心跳的次数通常和人的年龄有关,如果用![]() 表示一个人的年龄,用
表示一个人的年龄,用![]() 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么
表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么![]()
(1)正常情况下,在运动时一个20岁的人所能承受的每分钟心跳的最高次数是多少?
(2)一个50岁的人运动时10秒心跳的次数为23,请问他有危险吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了创建书香校园,去年又购进了一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等,求去年购进的文学书和科普书的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A. 1:2:3:4 B. 1:2:1:2 C. 1:1:2:2 D. 1:2:2:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
A. 正数和负数互为相反数
B. 任何一个数的相反数都与它本身不相同
C. 任何一个数都有它的相反数
D. 数轴上原点两旁的两个点表示的数互为相反数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com