

分析 (1)过点F作FH⊥OA,垂足为H,得出FH=HA,设FH=HA=x,则OH=7-x,在Rt△OHF中运用勾股定理求出x的值,继而可得AF的长.
(2)由(1)可知,点F的坐标是(3,4)或(4,3),结合tan∠FOA=$\frac{4}{3}$,确定F的坐标是(3,4),过点F作FH⊥OA于点H,当点P1落在x轴的正半轴上时,有△DOF∽△DFP1,当点P2落在x轴的负半轴上时,有△DOF∽△FOP2,运用相似三角形的性质可得点P的坐标.
解答 解:(1) 如图1,过点F作FH⊥OA,垂足为H,
如图1,过点F作FH⊥OA,垂足为H,
∵四边形OABC为矩形,
∴∠OAB=90°,
∵AG平分∠OAB,
∴∠OAG=45°,
∴FH=HA,
∵OH2+FH2=OF2,
∴(7-x)2+x2=52,
解得:x1=3,x2=4,
∴AF=$\sqrt{2}$x=3$\sqrt{2}$或4$\sqrt{2}$;
(2)由(1)可知,点F的坐标是(3,4)或(4,3),
∵tan∠FOA=$\frac{4}{3}$,
∴F的坐标是(3,4),
如图2,过点F作FH⊥OA于点H,
且DF2=DH2+FH2=42+42=32,OF2=OH2+FH2=32+42=25,
∵∠FOA=∠FDO+∠DFO,∠FDO+∠FPO=∠FOA,
∴∠DFO=∠FPO,
①当点P1落在x轴的正半轴上时,有△DOF∽△DFP1,∴$\frac{DF}{D{P}_{1}}$=$\frac{DO}{DF}$,
∴DF2=DO•DP1,
∴DP1=32,
∴OP1=31,即P1(31,0);
②当点P2落在x轴的负半轴上时,有△DOF∽△FOP2,
∴$\frac{OF}{O{P}_{2}}$=$\frac{DO}{OF}$,
∴OF2=DO•0P2,
∴OP2=25,
∴P2(-25,0).
∴点P的坐标为:P1(31,0);P2(-25,0).
点评 本题考查了四边形的综合应用,涉及了勾股定理、相似三角形的判定与性质等知识,解答本题的关键是分类讨论思想及数形结合思想的运用,难度较大.


科目:初中数学 来源: 题型:解答题
 一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗
一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AB}{AP}$=$\frac{AC}{AB}$ | D. | $\frac{AB}{BP}$=$\frac{AC}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
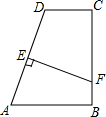 如图,在四边形ABCD中,∠B=∠C=90°,点E是AD的中点,EF⊥AD交CB于点F,DC=6,AB=8,BC=10,则线段BF的长为( )
如图,在四边形ABCD中,∠B=∠C=90°,点E是AD的中点,EF⊥AD交CB于点F,DC=6,AB=8,BC=10,则线段BF的长为( )| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{36}{5}$ | D. | $\frac{18}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.
如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,-2) | B. | (2,-1) | C. | (1,-2) | D. | (-2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com