
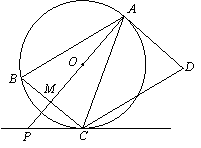
如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C与圆O相切的直线于点P。
(1)判断ÐBCP与ÐACD的数量关系,并说明理由。
(2)若AB=9,BC=6,求PC的长。
 |
(1) ÐBCP=ÐACD,
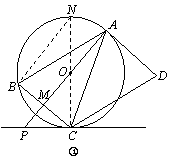
理由:如图j,连接CO并延长,交圆O于点N,连接BN。 ∵AB//CD,∴ÐBAC=ÐACD。
∵CN是圆O的直径,∴ÐCBN=90°。∴ÐBNC+ÐBCN=90°,
 ∵直线PC与圆O相切∴ÐPCO=90°,∴ÐBCP+ÐBCN=90°。
∵直线PC与圆O相切∴ÐPCO=90°,∴ÐBCP+ÐBCN=90°。
∴ÐBNC=ÐBCP。
又∵ÐBAC=ÐBNC,ÐBAC=ÐACD, 即ÐBCP=ÐACD
(2)∵AD是圆O的切线,∴AD^OA,即ÐOAD=90°。
∵BC//AD,∴ÐOMC=180°-ÐOAD=90°,即OM^BC。
∴MC=MB。∴AB=AC。
在Rt△AMC中,ÐAMC=90°,AC=AB=9,MC= 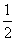 BC=3,
BC=3,
由勾股定理,得AM=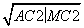 =
=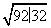 =6
=6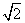 。
。
设圆O的半径为r。在Rt△OMC中,ÐOMC=90°,OM=AM-AO=6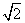 -r,MC=3,OC=r,
-r,MC=3,OC=r,
由勾股定理,得OM 2+MC 2=OC 2,即(6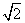 -r)2+32=r2。解得r=
-r)2+32=r2。解得r= 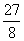
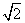 。
。
在△OMC和△OCP中, ∵ÐOMC=ÐOCP,ÐMOC=ÐCOP,
∴△OMC~△OCP。 ∴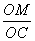 =
= 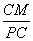 ,即
,即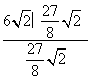 =
= 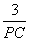 。
。
∴PC= 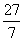 。
。


科目:初中数学 来源: 题型:
设点P是△ABC内任意一点.现给出如下结论:
①过点P至少存在一条直线将△ABC分成周长相等的两部分;
②过点P至少存在一条直线将△ABC分成面积相等的两部分;
③过点P至多存在一条直线将△ABC分成面积相等的两部分;
④△ABC内存在点Q,过点Q有两条直线将其平分成面积相等的四个部分.
其中结论正确的是 .(写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题:①三角形的内心到三角形三个顶点的距离相等;②如果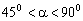 ,那么
,那么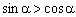 ;③若关于
;③若关于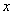 的方程
的方程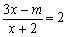 的解是负数,则m的取值范围为m<-4;④相等的圆周角所对的弧相等;⑤对于反比例函数
的解是负数,则m的取值范围为m<-4;④相等的圆周角所对的弧相等;⑤对于反比例函数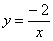 ,当
,当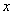 ﹥-1时,y随着x的增大而增大;其中正确命题有( )
﹥-1时,y随着x的增大而增大;其中正确命题有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,以原点O为圆心半径为10的圆,直线y=mx-4m+3与⊙O交于A、B两点,则弦AB的长的最小值为( )
A.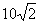 B.
B.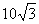 C.16 D. 20
C.16 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC中,AB=AC,∠A=36°.
(1)尺规作图:在AC上求作一点P,使BP+PC=AB.(保留作图痕迹,不写作法)
(2)在已作的图形中,连接PB, 若AB=2cm,求底边BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com