
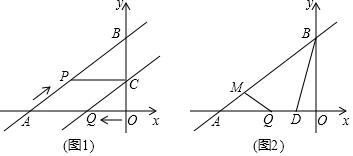
·ÖĪö £Ø1£©ÓÉ”÷ABO”×”÷QCO£¬ĶĘ³ö$\frac{AB}{QC}$=$\frac{AO}{QO}$£¬ĶĘ³ö$\frac{5}{QC}$=$\frac{4}{0.8t}$£¬ĶĘ³öQC=t£¬ÓÉAP=t£¬æɵĆAP=QC£¬AP”ĪQC£¬¼“æÉÖ¤Ć÷£®
£Ø2£©µ±ĖıߊĪŹ½APCQŹĒĮāŠĪŹ±£¬ŌņÓŠAP=AQ£¬ŌņæɵƵ½¹ŲÓŚtµÄ·½³Ģ£¬æÉĒóµĆtµÄÖµ£»
£Ø3£©ČēĶ¼2ÖŠ£¬ÓÉĢāŅāM£Ø-3£¬$\frac{3}{4}$£©£¬½«µćMĻņÓŅĘ½ŅĘ1øöµ„Ī»µĆµ½M”ä£Ø-2£¬$\frac{3}{4}$£©£¬×÷µćM”ä¹ŲÓŚOAµÄ¶Ō³ĘµćM”å£Ø-2£¬-$\frac{3}{4}$£©£¬Į¬½ÓBM”å½»OAÓŚD£¬“ĖŹ±ĖıߊĪMQDBµÄÖܳ¤×ī¶Ģ£¬Ēó³öÖ±ĻßBM”åµÄ½āĪöŹ½£¬æɵƵćD×ų±ź£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
½ā“š ½ā£ŗ£Ø1£©½įĀŪ£ŗĖıߊĪAPCQŹĒĘ½ŠŠĖıߊĪ£®ĄķÓÉČēĻĀ£ŗ
”ßÖ±Ļßy=$\frac{3}{4}$x+3ÓėxÖį”¢yÖį·Ö±š½»ÓŚµćA”¢B£¬
”ąA£Ø-4£¬0£©£¬B£Ø0£¬3£©£¬
”ąOA=4£¬OB=3£¬AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5£®
”ßQC”ĪAB£¬
”ą”÷ABO”×”÷QCO£¬
”ą$\frac{AB}{QC}$=$\frac{AO}{QO}$£¬
”ą$\frac{5}{QC}$=$\frac{4}{0.8t}$£¬
”ąQC=t£¬
”ßAP=t£¬
”ąAP=QC£¬”ßAP”ĪQC£¬
”ąĖıߊĪAPCQŹĒĘ½ŠŠĖıߊĪ£®
£Ø2£©”ßĖıߊĪAPCQŹĒĘ½ŠŠĖıߊĪ£¬
”ąµ±AP=AQŹ±£¬ĖıߊĪAPCQŹĒĮāŠĪ£¬
”ąt=4-0.8t£¬
”ąt=$\frac{20}{9}$s£¬
”ąµ±tĪŖ$\frac{20}{9}$sŹ±£¬ĖıߊĪAPCQŹĒĮāŠĪ£®
£Ø3£©ČēĶ¼2ÖŠ£¬ÓÉĢāŅāM£Ø-3£¬$\frac{3}{4}$£©£¬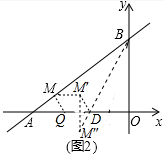
½«µćMĻņÓŅĘ½ŅĘ1øöµ„Ī»µĆµ½M”ä£Ø-2£¬$\frac{3}{4}$£©£¬×÷µćM”ä¹ŲÓŚOAµÄ¶Ō³ĘµćM”å£Ø-2£¬-$\frac{3}{4}$£©£¬Į¬½ÓBM”å½»OAÓŚD£¬“ĖŹ±ĖıߊĪMQDBµÄÖܳ¤×ī¶Ģ£¬
ÉčÖ±ĻßBM”åµÄ½āĪöŹ½ĪŖy=kx+b£¬ŌņÓŠ$\left\{\begin{array}{l}{b=3}\\{-2k+b=-\frac{3}{4}}\end{array}\right.$£¬
½āµĆ$\left\{\begin{array}{l}{k=\frac{15}{8}}\\{b=3}\end{array}\right.$£¬
”ąÖ±ĻßBM”åµÄ½āĪöŹ½ĪŖy=$\frac{15}{8}$x+3£¬Įīy=0µĆµ½x=-$\frac{8}{5}$£¬
”ąD£Ø-$\frac{8}{5}$£¬0£©£¬
”ąOQ=1+$\frac{8}{5}$=$\frac{13}{5}$£¬
”ąt=$\frac{13}{5}$”Ā0.8=$\frac{13}{4}$s£¬
ĖıߊĪMQDBµÄÖܳ¤µÄ×īŠ”Öµ=MQ+QD+DB+BM
=DQ+DMӊ+BD+BM
=QD+MӌD+DB+BM
=QD+BMӌ+BM
=1+$\sqrt{{2}^{2}+£Ø3+\frac{3}{4}£©^{2}}$+$\sqrt{{3}^{2}+£Ø3-\frac{3}{4}£©^{2}}$
=1+$\frac{17}{4}$+$\frac{15}{4}$=9£®
µćĘĄ ±¾Ģāæ¼²éŅ»“ĪŗÆŹż×ŪŗĻĢā”¢Ę½ŠŠĖıߊĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢ĮāŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢¹“¹É¶ØĄķ”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įĄūÓƶŌ³Ę”¢Ę½ŅʵČÖŖŹ¶½ā¾ö×ī¶ĢĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ČżŠĀæģ³µ½šÅĘÖÜÖÜĮ·ĻµĮŠ“š°ø
ČżŠĀæģ³µ½šÅĘÖÜÖÜĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
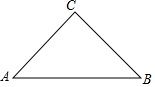 ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬CA=CB=4£¬½«”÷ABC·ÕŪ£¬Ź¹µĆµćBÓė±ßACµÄÖŠµćMÖŲŗĻ£¬Čē¹ūÕŪŗŪÓė±ßABµÄ½»µćĪŖE£¬ÄĒĆ“BEµÄ³¤ĪŖ$\frac{5\sqrt{2}}{3}$£®
ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬CA=CB=4£¬½«”÷ABC·ÕŪ£¬Ź¹µĆµćBÓė±ßACµÄÖŠµćMÖŲŗĻ£¬Čē¹ūÕŪŗŪÓė±ßABµÄ½»µćĪŖE£¬ÄĒĆ“BEµÄ³¤ĪŖ$\frac{5\sqrt{2}}{3}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | k£¾-7 | B£® | k”Ż-7 | C£® | k”Ż0 | D£® | k”Ż1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
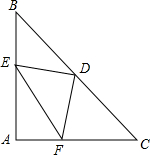 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻA=90”ć£¬µćDŹĒBC±ßµÄÖŠµć£¬µćE£¬F·Ö±šŌŚAB£¬ACÉĻ£®ĒŅDE”ĶDF£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻA=90”ć£¬µćDŹĒBC±ßµÄÖŠµć£¬µćE£¬F·Ö±šŌŚAB£¬ACÉĻ£®ĒŅDE”ĶDF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā

| A£® | 2018 | B£® | 2017 | C£® | 2016 | D£® | 2015 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ÉŁ24 | B£® | ¶ą24 | C£® | ÉŁ4 | D£® | ¶ą4 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼ĖłŹ¾ĪŖŅ»øöÕż·½Ģå½ŲČ„Į½øö½ĒŗóµÄĮ¢ĢåĶ¼ŠĪ£¬Čē¹ūÕÕÕāŃł½ŲČ”Õż·½ĢåµÄ°Ėøö½Ē£¬ŌņŠĀµÄ¼øŗĪĢåµÄĄāÓŠ¶ąÉŁĢõ£æĒėĖµĆ÷ÄćµÄĄķÓÉ£®
ČēĶ¼ĖłŹ¾ĪŖŅ»øöÕż·½Ģå½ŲČ„Į½øö½ĒŗóµÄĮ¢ĢåĶ¼ŠĪ£¬Čē¹ūÕÕÕāŃł½ŲČ”Õż·½ĢåµÄ°Ėøö½Ē£¬ŌņŠĀµÄ¼øŗĪĢåµÄĄāÓŠ¶ąÉŁĢõ£æĒėĖµĆ÷ÄćµÄĄķÓÉ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com