
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点A﹙2,4﹚、C﹙4,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙2,4﹚、C﹙4,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的![]() 的取值范围 .
的取值范围 .

【答案】(1)![]() ;(2)6;(3)-2<x<0或x>4
;(2)6;(3)-2<x<0或x>4
【解析】
(1)把点A(-2,-4)代入反比例函数的解析式,求出m的值,得到反比例函数不含m的解析式,把点C(4,n)代入反比例函数解析式,求出n的值,从而得到点C的坐标,用待定系数法求出一次函数的表达式即可;
(2)根据(1)求得的反比例函数求得点B和点D的坐标,将△AOC看作△AOB,△BOD的面积和△COD的和,分别计算面积,再求和,即可得到答案;
(3)根据函数图象,写出当x值相同时,一次函数的值大于反比例函数的值的x的取值范围即可.
解:(1)把点A(-2,-4)代入反比例函数的解析式![]() 得:-4=
得:-4=![]() ,
,
解得:m=10,
即反比例函数的解析式为:y=![]() ,
,
把点C(4,n)代入解析式y=![]() 得:n=2,
得:n=2,
∴点C的坐标为(4,2),
把点A(-2,-4)和点C(4,2)代入y=kx+b得:
![]() ,
,
解得:
![]() ,
,
∴一次函数的表达式为y=x-2;
(2)把x=0代入y=x-2得:y=-2,
即OB=2,
把y=0代入y=x-2得:x=2,
即OD=2,
∵A(-2,-4),C(4,2),
∴点A到y轴的距离为2,点C到x轴的距离为2,
∴△AOB的面积=![]() ×2×2=2,
×2×2=2,
△BOD的面积=![]() ×2×2=2,
×2×2=2,
△COD的面积=![]() ×2×2=2,
×2×2=2,
△AOC的面积=△AOB的面积+△BOD的面积+△COD的面积=6,
即AOC的面积为6;
(3)通过观察图象可知:
使一次函数的值大于反比例函数的x的取值范围为:-2<x<0或x>4.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】填写证明的理由:
已知,如图AB∥CD,EF、CG分别是∠ABC、∠ECD的角平分线.
求证:EF∥CG
证明:∵AB∥CD(已知)
∴∠AEC=∠ECD( )
又EF平分∠AEC、CG平分∠ECD(已知)
∴∠1=![]() ∠ ,∠2=
∠ ,∠2=![]() ∠ (角平分线的定义)
∠ (角平分线的定义)
∴∠1=∠2( )
∴EF∥CG( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )


A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图案由边长相等的黑,白两色正方形按一定规律拼接而成,设第![]() 个图案中白色小正方形的个数为
个图案中白色小正方形的个数为![]() .
.
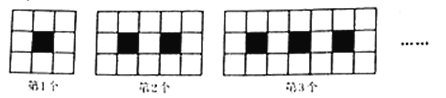
(1)第2个图案中有______个白色的小正方形;第3个图案中有______个白色的小正方形;![]() 与
与![]() 之间的函数表达式为______(直接写出结果).
之间的函数表达式为______(直接写出结果).
(2)是否存在这样的图案,使白色小正方形的个数为2019个?如果存在,请指出是第几个图案;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学要测量学校的国旗杆BD的高度.如图,学校的国旗杆与教学楼之间的距AB=20m.小明在教学楼三层的窗口C测得国旗杆顶点D的仰角为14°,旗杆底部B的俯角为22°.
(1)求∠BCD的大小.
(2)求国旗杆BD的高度(结果精确到1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,其中a,b满足
,其中a,b满足![]()

(1)填空:a= ,b= ;
(2)如果在第三象限内有一点C(-2,m),请用含m的式子表示△ABC的面积;
(3)在⑵条件下,当![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月14日,备受关注的《成都市中小学课后服务实施意见》正式出台.某区为了解“家长更希望如何安排孩子放学后的时间”,对该区七年级部分家长进行了一次问卷调查(每位同学只选择一位家长参与调查),将调查结果(![]() .回家,家人陪伴;
.回家,家人陪伴;![]() .学校课后延时服务;
.学校课后延时服务;![]() .校外培训机构;
.校外培训机构;![]() .社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)本次调查的家长总人数为 ;
(2)补全条形统计图:扇形统计图中,![]() 类所对应的圆心角为 度;
类所对应的圆心角为 度;
(3)若该区共有七年级学生![]() 人,则愿意参加“学生课后延时服务”的人数大概是多少?
人,则愿意参加“学生课后延时服务”的人数大概是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
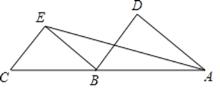
【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com