
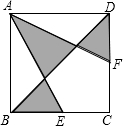
 已知正方形ABCD,E为BC的中点,DF=$\frac{1}{2}$CF,求阴影部分占正方形面积的几分之几?
已知正方形ABCD,E为BC的中点,DF=$\frac{1}{2}$CF,求阴影部分占正方形面积的几分之几? 分析 连接CM,CN,利用正方形的性质和全等三角形的判定定理易得△ADN≌△CDN,根据DF=$\frac{1}{2}CF$,易得△ADF的面积,△DNF的面积为△ADN面积的$\frac{1}{3}$,易得△DNF的面积,△ADN的面积,同理可得△BEM与△ABM的面积,易得△AMN的面积,从而得出阴影部分的面积,得出结论.
解答 解:连接CM,CN,
∵四边形ABCD为正方形,
∴AD=CD,∠ADN=∠CDN=45°,
在△ADN与△CDN中,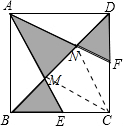
$\left\{\begin{array}{l}{AD=CD}\\{∠ADN=∠CDN}\\{DN=DN}\end{array}\right.$,
∴△ADN≌△CDN,
∴S△ADN=S△CDN,
设正方形的边长为a,
∵DF=$\frac{1}{2}CF$,
∴DF=$\frac{1}{3}DC$=$\frac{1}{3}a$,
∴S△ADF=$\frac{1}{2}$×$\frac{1}{3}a×a$=$\frac{1}{6}$a2,S△DNF=$\frac{1}{3}$S△DNC=$\frac{1}{3}$S△ADN,
∴S△ADN=3S△DNF,
∴S△ADF=4S△DNF=$\frac{1}{6}$a2,
∴S△DNF=$\frac{1}{24}$a2,S△ADN=$\frac{1}{6}{a}^{2}$-$\frac{1}{24}{a}^{2}$=$\frac{1}{8}{a}^{2}$,
同理可得,△ABM≌△CBM,
S△ABE=$\frac{1}{2}$×$\frac{1}{2}a×a$=$\frac{1}{4}$a2,
S△BEM=$\frac{1}{2}$S△BMC=$\frac{1}{2}$S△ABM,
∴S△ABM=2S△BEM,
∴3S△BEM=S△ABE=$\frac{1}{4}{a}^{2}$,
∴S△BEM=$\frac{1}{12}$a2,
∴S△ABM=$\frac{1}{4}{a}^{2}$-$\frac{1}{12}{a}^{2}$=$\frac{1}{6}{a}^{2}$
∵S△AMN=S△ABD-S△ABM-S△ADN=$\frac{1}{2}$a2-$\frac{1}{6}{a}^{2}$-$\frac{1}{8}{a}^{2}$=$\frac{5}{24}{a}^{2}$,
∴S阴影=$\frac{5}{24}{a}^{2}$+$\frac{1}{12}{a}^{2}$+$\frac{1}{24}{a}^{2}$=$\frac{1}{3}{a}^{2}$,
∵S正方形=a2,
∴阴影部分占正方形面积的$\frac{1}{3}$.
点评 此题考查了全等三角形的判定与性质与正方形的性质,注意掌握等高三角形面积的比等于底的比是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.
如图,矩形ABCD的面积S,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOnCn+1B的面积为$\frac{S}{{2}^{n+1}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
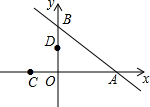 如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
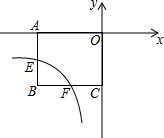 如图,反比例函数y=$\frac{k}{x}$与矩形OABC交于E、F两点,其中E为AB的中点,S△OBF=$\frac{9}{2}$,则k=-6.
如图,反比例函数y=$\frac{k}{x}$与矩形OABC交于E、F两点,其中E为AB的中点,S△OBF=$\frac{9}{2}$,则k=-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com