
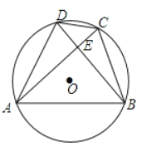
【题目】如图,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)若![]() ,则
,则![]() °.
°.
(2)求证: ![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)110;(2)见解析;(3)![]()
【解析】
(1)由等腰三角形的性质求出∠ABC和∠ACB的度数,然后根据圆内接四边形的性质即可求出∠ADC的值;
(2)设![]() ,由等腰三角形的性质求表示出∠ABC和∠ACB,进而得出∠CBD,由圆周角定理得出∠DAC=∠CBD=
,由等腰三角形的性质求表示出∠ABC和∠ACB,进而得出∠CBD,由圆周角定理得出∠DAC=∠CBD=![]() ,即可得出结论;
,即可得出结论;
(3)由△ECD∽△EBA,可得BE=2CE,设CE=x,则BE=2x,AE=10-x,
在Rt△ABE中,求出x的值,再在Rt△BCE中即可求出BC的值.
解:(1)∵AB=AC,![]() ,
,
∴∠ABC=∠ACB=70°,
∵四边形![]() 内接于⊙
内接于⊙![]() ,
,
∴∠ADC=180°-70°=110°;
(2)设![]() ,
,
∵AB=AC,
∴∠ABC=∠ACB=![]() ,
,
∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠CBD=90°-![]() =
=![]() ,
,
∵∠DAC=∠CBD,
∴![]() ;,
;,
(3)∵∠ACD=∠ABD,∠BDC=∠BAC,
∴△ECD∽△EBA,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴BE=2CE,
设CE=x,则BE=2x,AE=10-x,
在Rt△ABE中,
(10-x)2+(2x)2=102,
解得
x1=4,x2=0(舍去),
∴CE=4,BE=8,
∴BC=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
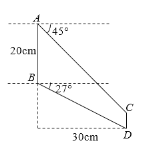
【题目】某校航模小组打算制作模型飞机,设计了如图所示的模型飞机机翼图纸.图纸中AB∥CD,均与水平方向垂直,机翼前缘AC、机翼后缘BD与水平方向形成的夹角度数分别为45°、27°,AB=20cm,点D到直线AB的距离为30cm.求机翼外缘CD的长度.(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰Rt△ABC和等腰Rt△AED中,∠ACB=∠AED=90°,且AD=AC.

(1)发现:如图1,当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN与EC的位置关系是 ,MN与EC的数量关系是 .
(2)探究:若把(1)小题中的△AED绕点A顺时针旋转45°得到的图2,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
(3)若把(1)小题中的△AED绕点A逆时针旋转45°得到的图3,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
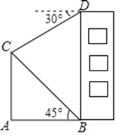
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字0,1,2,3的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽出一张卡片,则抽到数字“2”的概率为 ;
(2)随机抽出一张卡片,记下数字后放回并搅匀,再随机抽出一张卡片,请用列表或画树状图的方法,求两次抽出的卡片上的数字之和是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
A:自带白开水;B:瓶装矿泉水;C:碳酸饮料;D:非碳酸饮料.
根据统计结果绘制如下两个统计图(如图),根据统计图提供的信息,解答下列问题:
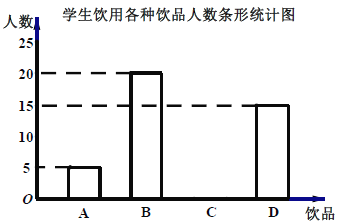
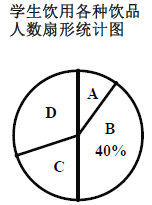
(1)请你补全条形统计图;
(2)在扇形统计图中,求“碳酸饮料”所在的扇形的圆心角的度数;
(3)为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学担任生活监督员,请用列表法或树状图法求出恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的数字支付正在引领未来世界的支付方式变革.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
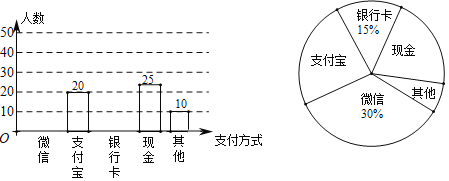
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表的方法,求两人选同种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com