
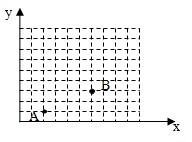
 17、如图,已知A、B两个村庄的坐标分别是(2,1)和(6,3),一辆汽车从原点O出发,沿x轴向右行驶.
17、如图,已知A、B两个村庄的坐标分别是(2,1)和(6,3),一辆汽车从原点O出发,沿x轴向右行驶.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知A、B两个村庄在河流CD的同侧,它们到河的距离分别为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂P,向A、B两村供水,已知铺设水管的费用为每千米2万元,请你在河流CD上选择水厂的位置P,使铺设水管的费用最节省(只需正确找出P点位置即可,不需证明),并求出此时的总费用.
如图,已知A、B两个村庄在河流CD的同侧,它们到河的距离分别为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂P,向A、B两村供水,已知铺设水管的费用为每千米2万元,请你在河流CD上选择水厂的位置P,使铺设水管的费用最节省(只需正确找出P点位置即可,不需证明),并求出此时的总费用.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 x2-mx+
x2-mx+ m2(m≠0)的对称轴交x轴于点P,交反比例函数y=
m2(m≠0)的对称轴交x轴于点P,交反比例函数y= (k>0)图象于点Q,连接OQ.
(k>0)图象于点Q,连接OQ. k=2时,求证:△OPQ为等腰直角三角形;
k=2时,求证:△OPQ为等腰直角三角形; (k>0)图象交正方形OABC的边BC、BA于M、N两点,连接AQ、BQ,有S△ABQ=4S△APQ.
(k>0)图象交正方形OABC的边BC、BA于M、N两点,连接AQ、BQ,有S△ABQ=4S△APQ.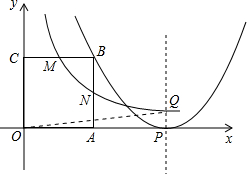
查看答案和解析>>
科目:初中数学 来源:2013年江苏省无锡市南长区宜兴市中考数学二模试卷(解析版) 题型:解答题
 x2-mx+
x2-mx+ m2(m≠0)的对称轴交x轴于点P,交反比例函数y=
m2(m≠0)的对称轴交x轴于点P,交反比例函数y=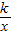 (k>0)图象于点Q,连接OQ.
(k>0)图象于点Q,连接OQ. k=2时,求证:△OPQ为等腰直角三角形;
k=2时,求证:△OPQ为等腰直角三角形;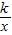 (k>0)图象交正方形OABC的边BC、BA于M、N两点,连接AQ、BQ,有S△ABQ=4S△APQ.
(k>0)图象交正方形OABC的边BC、BA于M、N两点,连接AQ、BQ,有S△ABQ=4S△APQ.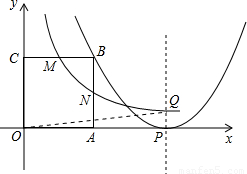
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com