Question

19．如图，在菱形ABCD中，AB=10，∠ABC=60°．动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动；动点Q从点D出发沿折线DC-CA-AB以每秒3个单位长的速度匀速运动，过点P作PF⊥BC，交折线AB-AC于点E，交直线AD于点F．若P、Q两点同时出发，当其中一点到达终点时整个运动随之停止，设运动时间为t秒．
（1）如图①，若Q在线段DC上运动时，当=3，QE⊥AB；
（2）如图②，设△PQE的面积为S，请求出S与t的函数关系式；
（3）如图③，在整个运动过程中（不包括动点的起始位置），是否存在时刻t，使得△PQF为直角三角形？若存在，请直接写出此时t的值；若不存在，说明理由

Answer 1

分析 （1）当点Q在DC上时，如图1中，作CM⊥AB于M．在Rt△CBM中，根据BC=2BM=2（BE-QC），列出方程即可解决问题．
（2）分五种情形①当0≤t≤$\frac{10}{3}$时，点Q在DC上，点E在AB上，如图2中，②当$\frac{10}{3}$＜t≤5时，点Q在CA上，点E在AB上，如图3中，③5＜t≤6时，点Q、E都在AC上时，且Q在E的右侧，如图4中，④当6＜t≤$\frac{20}{3}$时，点Q、E都在CA上，且点Q在EP的左侧，如图5中，⑤当$\frac{20}{3}$＜t≤10时，点Q在AB上，点E在CA上时，如图6中，分别求解即可．
（3）分四种情形①当P与C重合时，△QPF是直角三角形．②当点Q在AC上，点E在AB上时，如图7中，过点Q作MN⊥BC于M交AD于N．由△FNQ∽△QMP，得$\frac{NQ}{MP}$=$\frac{FN}{QM}$列出方程即可．③点Q与点A重合时，△PFQ是直角三角形．④当点Q在AB上，点E在AC上时，如图8中，过点Q作MN⊥BC于M交AD于N．利用相似三角形的性质列出方程求解即可．

解答 解：（1）当点Q在DC上时，如图1中，作CM⊥AB于M．

∵QE⊥AB，
∴CM∥EQ，CQ∥EM，
∴四边形CMEQ是平行四边形，
∵∠CME=90°，
∴四边形CMEQ是矩形，
∴CM=EQ，
在Rt△CBM中，∵∠B=60°，
∴∠BCM=30°
∴BC=2BM=2（BE-QC）
即10=2[2t-（10-3t）]，解得t=3所以，当t=3秒时，QE⊥AB．
故答案为3．

（2）①当0≤t≤$\frac{10}{3}$时，点Q在DC上，点E在AB上，如图2中，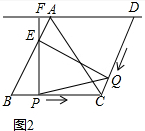

S=$\frac{1}{2}$×$\sqrt{3}$t×[10-t+$\frac{1}{2}$（10-3t）]=-$\frac{{5\sqrt{3}}}{4}$t²+$\frac{{15\sqrt{3}}}{2}$t，
②当$\frac{10}{3}$＜t≤5时，点Q在CA上，点E在AB上，如图3中，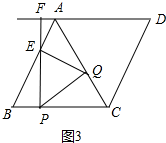

S=$\frac{1}{2}$×$\sqrt{3}$t×[10-t-$\frac{1}{2}$（3t-10）]=-$\frac{5\sqrt{3}}{4}$t²+$\frac{15\sqrt{3}}{2}$t，
③5＜t≤6时，点Q、E都在AC上时，且Q在E的右侧，如图4中，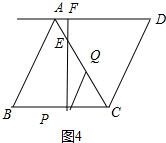

S=$\frac{1}{2}$×$\sqrt{3}$（10-t）×[10-t-$\frac{1}{2}$（3t-10）]=$\frac{{5\sqrt{3}}}{4}$t²-20$\sqrt{3}$t+75$\sqrt{3}$，

④当6＜t≤$\frac{20}{3}$时，点Q、E都在CA上，且点Q在EP的左侧，如图5中，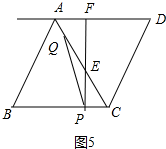

S=$\frac{1}{2}$×$\sqrt{3}$（10-t）×$\frac{1}{2}$[3t-10-2（10-t）]=-$\frac{{5\sqrt{3}}}{4}$t²+20$\sqrt{3}$t-75$\sqrt{3}$，
⑤当$\frac{20}{3}$＜t≤10时，点Q在AB上，点E在CA上时，如图6中，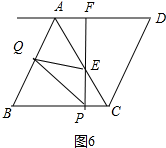

S=$\frac{1}{2}$×$\sqrt{3}$（10-t）×[t-5-$\frac{1}{2}$（3t-20）]=$\frac{\sqrt{3}}{4}$t²-5$\sqrt{3}$t+25$\sqrt{3}$．
综上所述S=$\left\{\begin{array}{l}{-\frac{5\sqrt{3}}{4}{t}^{2}+\frac{15\sqrt{3}}{2}t}&{（0≤t≤5）}\\{\frac{5\sqrt{3}}{4}{t}^{2}-20\sqrt{3}t+75\sqrt{3}}&{（5＜t≤6）}\\{-\frac{5\sqrt{3}}{4}{t}^{2}+20\sqrt{3}t-75\sqrt{3}}&{（6＜t≤\frac{20}{3}）}\\{\frac{\sqrt{3}}{4}{t}^{2}-5\sqrt{3}t+25\sqrt{3}}&{（\frac{20}{3}＜t≤10）}\end{array}\right.$．


（3）①当P与C重合时，△QPF是直角三角形，此时t=$\frac{10}{3}$．
②当点Q在AC上，点E在AB上时，如图7中，过点Q作MN⊥BC于M交AD于N．

∵∠FQP=90°，
∴∠FQN+∠PQM=90°，∠PQM+∠QPM=90°，
∴∠FQN=∠QPM，∵∠FNQ=∠PMQ=90°，
∴△FNQ∽△QMP，
∴$\frac{NQ}{MP}$=$\frac{FN}{QM}$，
∴$\frac{5\sqrt{3}-\frac{\sqrt{3}}{2}（3t-10）}{10-t-\frac{1}{2}（3t-10）}$=$\frac{10-t-\frac{1}{2}（3t-10）}{\frac{\sqrt{3}}{2}（3t-10）}$，
整理得到26t²-285t+750=0，
解得t=$\frac{285±5\sqrt{129}}{52}$．
③点Q与点A重合时，△PFQ是直角三角形，此时t=$\frac{20}{3}$，
④当点Q在AB上，点E在AC上时，如图8中，过点Q作MN⊥BC于M交AD于N

由△FNQ∽△QMP，
得$\frac{NQ}{MP}$=$\frac{FN}{QM}$，所以$\frac{\frac{\sqrt{3}}{2}（3t-20）}{t-\frac{1}{2}（30-3t）}$=$\frac{t-\frac{1}{2}（30-3t）}{\frac{\sqrt{3}}{2}（30-3t）}$，
整理得26t²-375t+1350=0，
∴（13t-90）（2t-15）=0，
∴t=$\frac{90}{13}$或$\frac{15}{2}$．

点评 本题考查四边形综合题、矩形的性质、等边三角形的性质、相似三角形的判定和性质等知识，解题的关键是学会分类讨论，不能漏解，学会把问题转化为方程的思想思考问题，属于中考压轴题．