Question

【题目】如图，已知△ABC和△CDE都是等边三角形，且A、C、E三点共线．AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下五个结论：① AD=BE；② ∠AOB=60°;③AP=BQ； ④△PCQ是等边三角形;⑤PQ∥AE．其中正确结论的有（　　）个

A.5B.4C.3D.2

Answer 1

【答案】A

【解析】

根据等边三角形的性质可得AC＝BC，CD＝CE，∠ACB＝∠DCE，再求出∠ACD＝∠BCE，然后利用“边角边”证明△ACD和△BCE全等，根据全等三角形对应边相等可得AD＝BE，判断出①正确，全等三角形对应角相等可得∠ADC＝∠BEC，∠CAD＝∠CBE，再求出∠ACP＝∠BCQ＝60°，然后利用“边角边”证明△ACP和△BCQ全等，根据全等三角形对应边相等可得AP＝BQ，CP＝CQ，判断出③正确，根据∠AOB=∠PAC+∠BEC=∠QBC+∠BEC=∠BCA=60°，判断出②正确；判断出△PCQ为等边三角形，判断出④正确，根据等边三角形的性质可得∠CPQ＝60°，得到∠ACB＝∠CPQ，再根据内错角相等，两直线平行可得PQ∥AE，判断出⑤正确.

∵△ABC和△CDE均是等边三角形，

∴AC＝BC，CD＝CE，∠ACB＝∠DCE，

∴∠ACB＋∠ACE＝∠DCE＋∠ACE，

即∠ACD＝∠BCE，

在△ACD和△BCE中，

，

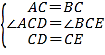∴△ACD≌△BCE（SAS），

∴AD＝BE，（故①正确）；

∴∠ADC＝∠BEC，∠CAD＝∠CBE，

∵∠BCQ＝180°2×60°＝60°，

∴∠ACP＝∠BCQ＝60°，

在△ACP和△BCQ中，

，

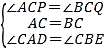∴△ACP≌△BCQ（ASA），

∴AN＝BM，CM＝CN，（故③正确）；

∵∠AOB=∠PAC+∠BEC=∠QBC+∠BEC=∠BCA=60°，

故②正确；

∵∠BCQ＝60°，CQ＝CP，

∴△PCQ是等边三角形，（故④正确）；

∴∠CPQ＝60°，

∴∠ACB＝∠CPQ＝60°，

∴PQ∥BD，（故⑤正确）；

综上所述，结论正确的是5个．

故选：A．