
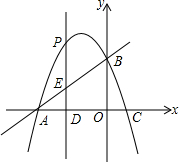
 在平面直角坐标系中,直线y=x+4与x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并于x轴交于另一点C(点C在点A的右侧),点P是抛物线上一动点.
在平面直角坐标系中,直线y=x+4与x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并于x轴交于另一点C(点C在点A的右侧),点P是抛物线上一动点.分析 (1)先由直线解析式求出A、B两点坐标,再将A、B两点坐标代入抛物线解析式求出b、c,进而确定C点坐标;
(2)P、E横坐标一样,PE的长度就是P点与E点的纵坐标之差,将P、E的纵坐标分别用横坐标表示出来,从而把PE长度表示成横坐标的二次函数,配方求出最大值.
解答 解:(1)∵y=x+4与x轴、y轴分别交于A、B两点,
∴A(-4,0),B(0,4),
∵抛物线y=-x2+bx+c经过A、B两点,
∴c=4,-16-4b+c=0,
∴b=-3,c=4,
∴抛物线的解析式为y=-x2+-3x+4,
∵y=-x2+-3x+4=-(x-1)(x+4),
∴C(1,0),
(2)设P点的坐标为(m,-m2-3m+4),则E点的坐标为(m,m+4),
∴PE=(-m2-3m+4)-(m+4)=-m2-3m+4-m-4=-m2-4m=-m2-4m-4+4=-(m+2)2+4,
∴当m=-2时,PE取得最大值4,
此时P点坐标为(-2,6),
即当P点坐标为(-2,6)时,PE最长=4.
点评 本题本查了待定系数法求二次函数解析式、线段长度的坐标表示方法、配方法求二次函数最值等知识点,难度不大.需要强调的是,第(2)问当中用两点的纵坐标之差表示竖直方向线段的长度这种方法非常重要,在求解类似问题时经常用到,要引起重视.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sin30°<sin45°<sin60° | B. | cos60°>cos45°>cos30° | ||
| C. | tan60°<tan45°<tan30° | D. | cot30°<cot45°<cot60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
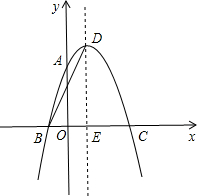 如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com