
����Ŀ��(10��)��һ����ֱ�Ĺ�·��������A��B��C������ׯ���ס�������ͬʱ�ֱ��A��B�������������Ħ�г�������綯���ع�·����ʻ��C�壬���յ���C�壮��ס������˵�C��ľ���y1��y2(km)����ʻʱ��x(h)֮��ĺ�����ϵ��ͼ��ʾ����ش��������⣺

(1)A��C�����ľ���Ϊ________km��a��________��
(2)���ͼ�е�P�����꣬�����õ���������ʾ��ʵ�����壻
(3)������ʻ�����У���ʱ���10km?
���𰸡�(1)120��2����2������������3��x��![]() h��x��
h��x��![]() h��x��
h��x��![]() hʱ
hʱ
�������������������1����ͼ��֪��y�ύ��������ʾA��C�����ľ���Ϊ120km������0.5Сʱ����C��90km����ʻ120-90=30km���ٶ�Ϊ60km/h�����a=2��
��2�����y1��y2������������ʽ���������̼�����õ�P���ꣻ
��3���ɣ�2���еĺ�������ʽ�����ݾ��10km�������̣�̽�ֵó��𰸼��ɣ�
�����������1��A��C�����ľ���120km��
a=120��[��120-90����0.5]=2��
�ʴ�Ϊ��120��2��
��2����y1=k1x+120��
���루2��0���ã�0=2k1+120��
��ã�k1=-60��
����y1=-60x+120��
��y2=k2x+90��
���루3��0���ã�0=3k2+90��
��ã�k2=-30��
����y2=-30x+90��
��-60x+120=-30x+90
���x=1����y1=y2=60��
����P��1��60����
��3����y1-y2=10��
��-60x+120-��-30x+90��=10��
���x=![]() ��
��
��y2-y1=10��
��-30x+90-��-60x+120��=10��
���x=![]() ��
��
�����ߵ�C�أ����Ҿ���C��10kmʱ��
-30x+90=10��
���x=![]() ��
��
������֪��x=![]() h����x=
h����x=![]() h����x=
h����x=![]() h�Ҿ��10km��
h�Ҿ��10km��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC����������ֱ�ΪA����1����2����B����2����4����C����4����1����
��1���ѡ�ABC����ƽ��3����λ��õ���A1B1C1���뻭����A1B1C1��д����B1�����ꣻ
B1( �� )
��2����ͨ������ƽ��![]() ����λ��������ƽ��
����λ��������ƽ��![]() ����λ���Ϳ��ѡ�ABCȫ���Ƶ���һ�����ڣ���д��
����λ���Ϳ��ѡ�ABCȫ���Ƶ���һ�����ڣ���д��![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ��
�� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC��������������ΪA����3��4����B����4��2����C����2��1����
��ABC��ԭ��˳ʱ����ת90�㣬�õ���A1B1C1����A1B1C1����ƽ��2����λ��������ƽ��5����
λ�õ���A2B2C2��
��1��������A1B1Cl�͡�A2B2C2��
��2��P��a��b���ǡ�ABC��AC����һ�㣬��ABC����ת��ƽ�ƺ��P�Ķ�Ӧ��ֱ�ΪP1��P2����
д����P1��P2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,һ������������ͼ����һ��һ�κ���ͼ���ڵ�A(3,4),��һ�κ�����ͼ����y���ཻ�ڵ�B(0,-5).

(1)�������������ı���ʽ;
(2)����AOB�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ϻ��������ԼΪ3500000 km2 �� �ÿ�ѧ��������ʾ��ȷ���ǣ� ��
A.3.5��105 km2
B.3.5��106 km2
C.3.5��107 km2
D.3.5��108 km2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ����kΪ������k��1����
����k������k��1����
��1������A��1��2�������������ͼ���ϣ���k��ֵ��
��2�������������ͼ���ÿһ��֧�ϣ�y��x�������������k��ȡֵ��Χ��
��3����k=13�����жϵ�B��3��4����C��2��5���Ƿ������������ͼ���ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
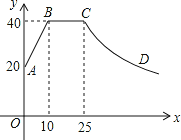
����Ŀ������ѧ���о����֣�һ������£�һ�ڿ�40�����У�ѧ����ע�������ʦ���εı仯���仯����ʼ�Ͽ�ʱ��ѧ����ע��������ǿ���м���һ��ʱ��ѧ����ע�������ֽ�Ϊ������ȶ�״̬�����ѧ����ע������ʼ��ɢ������ʵ�������֪��ѧ����ע����ָ��y��ʱ��x�����ӣ��ı仯��������ͼ��ʾ������AB��BC�ֱ�Ϊ�߶Σ�CDΪ˫���ߵ�һ���֣���
��1������߶�AB������CD�Ľ���ʽ����д���Ա�����ȡֵ��Χ��
��2����ʼ�Ͽκ�������ʱ�����ʮ����ʱ��Ƚϣ���ʱѧ����ע���������У�
��3��һ����ѧ�����⣬��Ҫ��19���ӣ�Ϊ��Ч���Ϻã�Ҫ��ѧ����ע����ָ����ʹﵽ36����ô�����ʵ����ţ���ʦ�ܷ���ѧ��ע�����ﵽ�����״̬�½����������Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E����AOB��ƽ������һ�㣬ED��OA��EC��OB������ֱ�ΪC��D��
��֤����1��OC=OD��
��2��OE���߶�CD�Ĵ�ֱƽ���ߣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����У�
���˽�һ����װʳƷ�Ƿ��з�������
���˽�ij��ѧ����50 ���ܡ��ijɼ���
���˽⽭�����ӡ��dz����š���Ŀ�������ʣ�
���˽�һ�����ݵ�ʹ��������
�ʺ����ղ飨ȫ����飩��ʽ���� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com