
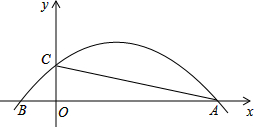
 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )| A. | (4,3) | B. | (5,$\frac{35}{12}$) | C. | (4,$\frac{35}{12}$) | D. | (5,3) |
分析 连接PC、PO、PA,设点P坐标(m,-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$),根据S△PAC=S△PCO+S△POA-S△AOC构建二次函数,利用函数性质即可解决问题.
解答 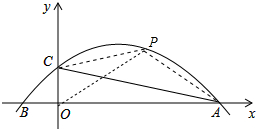 解:连接PC、PO、PA,设点P坐标(m,-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$)
解:连接PC、PO、PA,设点P坐标(m,-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$)
令x=0,则y=$\frac{5}{3}$,点C坐标(0,$\frac{5}{3}$),
令y=0则-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$=0,解得x=-2或10,
∴点A坐标(10,0),点B坐标(-2,0),
∴S△PAC=S△PCO+S△POA-S△AOC=$\frac{1}{2}$×$\frac{5}{3}$×m+$\frac{1}{2}$×10×(-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$)-$\frac{1}{2}$×$\frac{5}{3}$×10=-$\frac{5}{12}$(m-5)2+$\frac{125}{12}$,
∴x=5时,△PAC面积最大值为$\frac{125}{12}$,
此时点P坐标(5,$\frac{35}{12}$).
故点P坐标为(5,$\frac{35}{12}$).
点评 本题考查二次函数的性质、抛物线与x轴交点,解题的关键是构建二次函数,利用二次函数性质解决问题,属于中考常考题型.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:填空题
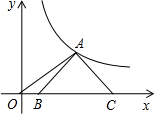 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
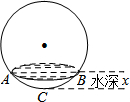 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )| A. | 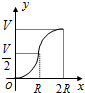 | B. | 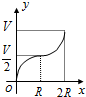 | C. | 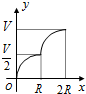 | D. | 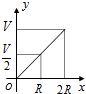 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=4,x2=-4 | B. | x1=2,x2=-2 | C. | x1=x2=0 | D. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com