
| A. | y=-2(x+1)2 | B. | y=-2(x+1)2+2 | C. | y=-2(x-1)2+2 | D. | y=-2(x-1)2+1 |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
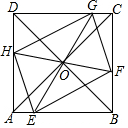 如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.
如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
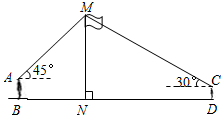 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数)
如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
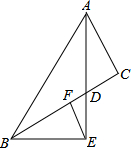 如图,△ABC中,AD是角平分线,BE⊥AD,垂足E在AD延长线上,F是BC的中点,AB=30cm,AC=18cm.则EF的长为6cm.
如图,△ABC中,AD是角平分线,BE⊥AD,垂足E在AD延长线上,F是BC的中点,AB=30cm,AC=18cm.则EF的长为6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com