
 阅读理解
阅读理解分析 (1)由在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$只有当a=b时,a+b有最小值2$\sqrt{p}$.即可得x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,则可求得答案;
(2)由y=$\frac{{{{(x+1)}^2}+2}}{x+1}$=(x+1)+$\frac{2}{x+1}$,直接利用a+b≥2$\sqrt{ab}$求解,即可求得答案;
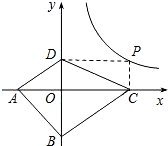
(3)首先设P的坐标为:(x,$\frac{6}{x}$),由S四边形ABCD=S△ABD+S△CBD,可得S四边形ABCD=$\frac{3}{2}$•(x+$\frac{4}{x}$+4),继而求得答案.
解答 解:(1)∵x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
∴当且仅当x=$\frac{1}{x}$,即x=1时,x+$\frac{1}{x}$有最小值2;
故答案为:1,2;
(2)∵y=$\frac{{{{(x+1)}^2}+2}}{x+1}$=(x+1)+$\frac{2}{x+1}$≥2$\sqrt{(x+1)•\frac{2}{x+1}}$=2$\sqrt{2}$,
∴当且仅当x+1=$\frac{2}{x+1}$,x=$\sqrt{2}$-1时,y的最小值为2$\sqrt{2}$;
(3)设P的坐标为:(x,$\frac{6}{x}$),
∵A(-2,0),B(0,-3),
则BD=3+$\frac{6}{x}$,OA=2,OC=x,
则S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$•2•(3+$\frac{6}{x}$)+$\frac{1}{2}$x•(3+$\frac{6}{x}$)=$\frac{3}{2}$•$\frac{(x+2)^{2}}{x}$=$\frac{3}{2}$•(x+$\frac{4}{x}$+4)≥$\frac{3}{2}$×(2$\sqrt{x•\frac{4}{x}}$+4)=12,
∴当且仅当x=$\frac{4}{x}$,即x=2时,四边形ABCD面积有最小值,最小值是12;
∴点P的坐标为:(2,3),
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是矩形.
点评 此题属于反比例函数综合题,考查了几何不等式的应用.理解在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$只有当a=b时,a+b有最小值2$\sqrt{p}$是关键.


科目:初中数学 来源: 题型:解答题
| 月 份 | 一月份 | 二月份 | 三月份 | 四月份 |
| 交费金额 | 76元 | 63元 | 45元6角 | 184元6角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知实数a、b、c在实数轴上对应点如图所示:
已知实数a、b、c在实数轴上对应点如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com