
”¾ĢāÄæ”æČēĶ¼1£¬ÉäĻß![]() ŌŚ
ŌŚ![]() µÄÄŚ²æ£¬Ķ¼ÖŠ¹²ÓŠ3øö½Ē£ŗ
µÄÄŚ²æ£¬Ķ¼ÖŠ¹²ÓŠ3øö½Ē£ŗ![]() £¬
£¬![]() ŗĶ
ŗĶ![]() £¬ČōĘäÖŠÓŠŅ»øö½ĒµÄ¶ČŹżŹĒĮķŅ»øö½Ē¶ČŹżµÄĮ½±¶£¬Ōņ³ĘÉäĻß
£¬ČōĘäÖŠÓŠŅ»øö½ĒµÄ¶ČŹżŹĒĮķŅ»øö½Ē¶ČŹżµÄĮ½±¶£¬Ōņ³ĘÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻߣ®
µÄĘęĆīĻߣ®
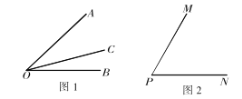
£Ø1£©ČēĶ¼1£¬ŌŚ![]() µÄÄŚ²æ£¬
µÄÄŚ²æ£¬![]() ÓŠ_________ĢõĘęĆīĻߣ»
ÓŠ_________ĢõĘęĆīĻߣ»
£Ø2£©ČēĶ¼2£¬Čō![]() £¬ÉäĻß
£¬ÉäĻß![]() Čʵć
Čʵć![]() “Ó
“Ó![]() Ī»ÖĆæŖŹ¼£¬ŅŌĆæĆė
Ī»ÖĆæŖŹ¼£¬ŅŌĆæĆė![]() µÄĖŁ¶ČÄꏱÕėŠż×Ŗ£¬µ±
µÄĖŁ¶ČÄꏱÕėŠż×Ŗ£¬µ±![]() Ź×“ĪµČÓŚ
Ź×“ĪµČÓŚ![]() Ź±Ķ£Ö¹Šż×Ŗ£¬É芿×ŖµÄŹ±¼äĪŖ
Ź±Ķ£Ö¹Šż×Ŗ£¬É芿×ŖµÄŹ±¼äĪŖ![]() £®
£®
¢ŁÖ±½ÓŠ“³öµ±![]() ĪŖŗĪÖµŹ±£¬ÉäĻß
ĪŖŗĪÖµŹ±£¬ÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻߣæ
µÄĘęĆīĻߣæ
¢ŚČōÉäĻß![]() Ķ¬Ź±Čʵć
Ķ¬Ź±Čʵć![]() ŅŌĆæĆė
ŅŌĆæĆė![]() µÄĖŁ¶ČÄꏱÕėŠż×Ŗ£¬²¢Óė
µÄĖŁ¶ČÄꏱÕėŠż×Ŗ£¬²¢Óė![]() Ķ¬Ź±Ķ£Ö¹Šż×Ŗ£®ĒėĒó³öµ±ÉäĻß
Ķ¬Ź±Ķ£Ö¹Šż×Ŗ£®ĒėĒó³öµ±ÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻߏ±
µÄĘęĆīĻߏ±![]() µÄÖµ£®
µÄÖµ£®
”¾“š°ø”æ£Ø1£©3£»£Ø2£©¢ŁtĪŖ4.5»ņ6»ņ9 £»¢Ś![]() »ņ
»ņ![]() »ņ
»ņ![]()
”¾½āĪö”æ
£Ø1£©øł¾ŻĘęĆīĻߵĶØŅ壬ČōOCŹĒÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻߣ¬ÓŠ”ĻAOB=2”ĻAOC”¢”ĻAOC=2”ĻBOC”¢”ĻBOC=2”ĻAOCČżÖÖĒéæö£»
µÄĘęĆīĻߣ¬ÓŠ”ĻAOB=2”ĻAOC”¢”ĻAOC=2”ĻBOC”¢”ĻBOC=2”ĻAOCČżÖÖĒéæö£»
£Ø2£©¢Ł±ķ“ļ³ö”ĻQPN”¢”ĻQPM=20”ćt-60”ć£¬ŌŁ·ÖČżÖÖĒéæö£¬øł¾ŻĘęĆīĻߵĶØŅåĮŠ³ö·½³Ģ¼“æÉĒó½ā£»
¢Ś±ķ“ļ³ö”ĻQPN”¢”ĻM”ÆPN”¢”ĻM”ÆPQ£¬ŌŁ·ÖČżÖÖĒéæö£¬øł¾ŻĘęĆīĻߵĶØŅåĮŠ³ö·½³Ģ¼“æÉĒó½ā£»
½ā£ŗ£Ø1£©Čō”ĻAOB=2”ĻAOC£¬ŌņOCŹĒÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻߣ¬
µÄĘęĆīĻߣ¬
Čō”ĻAOC=2”ĻBOC£¬ŌņOCŹĒÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻß
µÄĘęĆīĻß
Čō”ĻBOC=2”ĻAOC£¬ŌņOCŹĒÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻß
µÄĘęĆīĻß
”ąŌŚ![]() µÄÄŚ²æ£¬
µÄÄŚ²æ£¬![]() ÓŠ3ĢõĘęĆīĻߣ¬
ÓŠ3ĢõĘęĆīĻߣ¬
¹Ź“š°øĪŖ£ŗ3£®
£Ø2£©¢Ł”ß”ĻQPN=20”ćt£¬”ĻMPN=60”ć
”ą”ĻQPM=20”ćt-60”ć
µ±”ĻQPN=2”ĻMPNŹ±£¬¼“20”ćt=120”ć£¬½āµĆt=6s£¬
µ±”ĻQPM=2”ĻMPNŹ±£¬¼“20”ćt-60”ć=120”ć£¬½āµĆt=9s£¬
µ±”ĻMPN=2”ĻQPMŹ±£¬¼“60”ć=2£Ø20”ćt-60”ć£©£¬½āµĆt=4.5s£¬
¹Ź“š°øĪŖ£ŗtĪŖ4.5»ņ6»ņ9£®
¢ŚÓÉĢāŅāµĆ£ŗ”ĻQPN=20”ćt£¬”ĻM”ÆPN=60”ć+12”ćt£¬”ĻM”ÆPQ=60”ć-8”ćt
µ±![]() Ź±
Ź±
”ą![]()
”ą![]()
µ±![]() Ź±£¬
Ź±£¬
”ą![]()
”ą![]()
µ±![]() Ź±£¬
Ź±£¬
”ą![]()
”ą![]()
×ŪÉĻĖłŹö£¬µ±![]() »ņ
»ņ![]() »ņ
»ņ![]() Ź±£¬ÉäĻß
Ź±£¬ÉäĻß![]() ŹĒ
ŹĒ![]() µÄĘęĆīĻߣ®
µÄĘęĆīĻߣ®


 ŠĒ¼¶æŚĖćĢģĢģĮ·ĻµĮŠ“š°ø
ŠĒ¼¶æŚĖćĢģĢģĮ·ĻµĮŠ“š°ø Ć¢¹ū½ĢøØ“ļ±ź²āŹŌ¾ķĻµĮŠ“š°ø
Ć¢¹ū½ĢøØ“ļ±ź²āŹŌ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĒėøł¾ŻĶ¼ÖŠĢį¹©µÄÅÆĘæŗĶĖ®±µÄŹŪ¼ŪŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
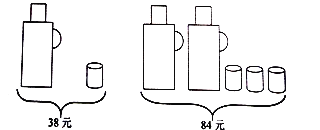
£Ø1£©Ņ»øöÅÆĘæÓėŅ»øöĖ®±µÄŹŪ¼Ū·Ö±šŹĒ¶ąÉŁŌŖ£æ
£Ø2£©¼×”¢ŅŅĮ½¼ŅÉĢ³”Ķ¬Ź±³öŹŪĶ¬ŃłµÄÅÆĘæŗĶĖ®±£¬ŌŚŠĀğʌ¼ä£¬Į½¼ŅÉĢ³”¶¼ŌŚøć“ŁĻś»ī¶Æ£®¼×ÉĢ³”¹ę¶Ø£ŗÕāĮ½ÖÖÉĢĘ·¶¼“ņ8.5ÕŪ£»ŅŅÉĢ³”¹ę¶Ø£ŗĮ½ÖÖÉĢĘ·¶¼²»“ņÕŪ£¬µ«ĀņŅ»øöÅÆĘæŌłĖĶŅ»øöĖ®±£®Čōijµ„Ī»ĻėŅŖĀņ4øöÅÆĘæŗĶ16øöĖ®±£¬ĒėĪŹÕāøöµ„Ī»Ń”ŌńÄļŅÉĢ³”¹ŗĀņøüŗĻĖć£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°“ČēĻĀ¹ęĀÉ°Ś·ÅČż½ĒŠĪ£ŗ
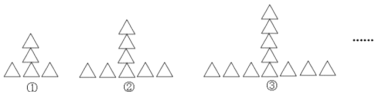
£Ø1£©Ķ¼¢ÜÖŠ·Ö±šÓŠ¶ąÉŁøöČż½ĒŠĪ£æ
£Ø2£©°“ÉĻŹö¹ęĀÉÅÅĮŠĻĀČ„£¬µŚnøöĶ¼ŠĪÖŠÓŠ¶ąÉŁøöČż½ĒŠĪ£æ
£Ø3£©°“ÉĻŹö¹ęĀÉÅÅĮŠĻĀČ„£¬µŚ2014øöĶ¼ŠĪÖŠÓŠ¶ąÉŁøöČż½ĒŠĪ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£ØĪŹĢāĒé¾³£©
ČēĶ¼1£¬ĖıߊĪABCDŹĒÕż·½ŠĪ£¬MŹĒBC±ßÉĻµÄŅ»µć£¬EŹĒCD±ßµÄÖŠµć£¬AEĘ½·Ö”ĻDAM£®ĒóÖ¤£ŗAM=AD+MC£®

£ØĢ½¾æÕ¹Ź¾£©
£Ø2£©ČōĖıߊĪABCDŹĒ³¤Óėæķ²»ĻąµČµÄ¾ŲŠĪ£¬ĘäĖūĢõ¼ž²»±ä£¬ČēĶ¼2£¬ŹŌÅŠ¶ĻAM=AD+MCŹĒ·ń³ÉĮ¢£æČō³ÉĮ¢£¬Ēėøų³öÖ¤Ć÷£¬Čō²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
£ØĶŲÕ¹ŃÓÉģ£©
£Ø3£©Čō£Ø2£©ÖŠ¾ŲŠĪABCDĮ½±ßAB=6£¬BC=9£¬ĒóAMµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø2015Öéŗ££©ŌĶĮ²ÄĮĻ£ŗÉĘÓŚĖ¼æ¼µÄŠ”¾üŌŚ½ā·½³Ģ×é![]() Ź±£¬²ÉÓĆĮĖŅ»ÖÖ”°ÕūĢå“ś»»”±µÄ½ā·Ø£ŗ½«·½³Ģ¢Ś±äŠĪ£ŗ4x+10y+y=5 ¼“2£Ø2x+5y£©+y=5¢Ū
Ź±£¬²ÉÓĆĮĖŅ»ÖÖ”°ÕūĢå“ś»»”±µÄ½ā·Ø£ŗ½«·½³Ģ¢Ś±äŠĪ£ŗ4x+10y+y=5 ¼“2£Ø2x+5y£©+y=5¢Ū
°Ń·½³Ģ¢Ł“ųČė¢ŪµĆ£ŗ2”Į3+y=5£¬”ąy=©1
°Ńy=©1“śČė¢ŁµĆx=4£¬”ą·½³Ģ×éµÄ½āĪŖ![]() £®
£®
ĒėÄć½ā¾öŅŌĻĀĪŹĢā£ŗ£Ø1£©Ä£·ĀŠ”¾üµÄ”°ÕūĢå“ś»»”±·Ø½ā·½³Ģ×é![]() £»
£»
£Ø2£©ŅŃÖŖx£¬yĀś×ć·½³Ģ×é![]() £®
£®
£Øi£©Ēó![]() µÄÖµ£»
掙术
£Øii£©Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
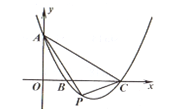
”¾ĢāÄæ”æČēĶ¼,Ę½ĆęÖ±½Ē×ų±źĻµÖŠ,Å×ĪļĻßy=-![]() x2-2x+3½»xÖįÓŚµćB,C,½»yÖįÓŚµćA,µćP(x,y)ŹĒÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć,Į¬½ÓPA,AC,PC,¼Ē”÷ACPĆ껿ĪŖS.µ±y”Ü3Ź±,SĖęx±ä»ÆµÄĶ¼Ļó“óÖĀŹĒ( )
x2-2x+3½»xÖįÓŚµćB,C,½»yÖįÓŚµćA,µćP(x,y)ŹĒÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć,Į¬½ÓPA,AC,PC,¼Ē”÷ACPĆ껿ĪŖS.µ±y”Ü3Ź±,SĖęx±ä»ÆµÄĶ¼Ļó“óÖĀŹĒ( )
A. 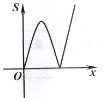 B.
B.  C.
C. 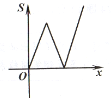 D.
D. 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖÉī»ÆæĪøÄ£¬Ā䏵Į¢µĀŹ÷ČĖÄæ±ź£¬Ä³Ń§Š£ÉčÖĆĮĖŅŌĻĀĖÄĆÅĶŲÕ¹ŠŌæĪ³Ģ£ŗA£®ŹżŃ§Ė¼Ī¬£¬B£®ĪÄѧ¼ųÉĶ£¬C£®ŗģ“¬æĪ³Ģ£¬D£®3D“ņÓ”£¬¹ę¶ØĆæĪ»Ń§ÉśŃ”±ØŅ»ĆÅ£®ĪŖĮĖ½āѧɜµÄ±ØĆūĒéæö£¬Ė껜³éČ”ĮĖ²æ·Öѧɜ½ųŠŠµ÷²é£¬²¢ÖĘ×÷³ÉČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēė»Ų“šĻĀĮŠĪŹĢā£ŗ
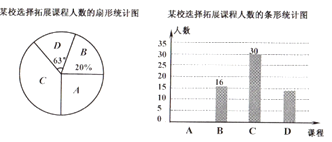
£Ø1£©ĒóÕā“Ī±»µ÷²éµÄѧɜČĖŹż£»
£Ø2£©Ēė½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©¼ŁČēČ«Š£ÓŠŃ§Éś1000ČĖ£¬Ēė¹Ą¼ĘŃ”±Ø”°ŗģ“¬æĪ³Ģ”±µÄѧɜČĖŹż.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com