
 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.当点P在线段AD上时速度是$\sqrt{5}$cm/s,在折线DE-EB上时速度是1cm/s.设点P的运动时间为t(s),且t>0,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.当点P在线段AD上时速度是$\sqrt{5}$cm/s,在折线DE-EB上时速度是1cm/s.设点P的运动时间为t(s),且t>0,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.分析 (1)根据勾股定理求出AB,根据D为AB中点,求出AD,根据点P在AD上的速度,即可求出点P在AD段的运动时间,再求出点P在DP段的运动时间,最后根据DE段运动速度为1cm/s,即可求出DP;
(2)点D与点N重合,P位于线段DE上,求出DP=DM=2,再根据DP=t-2,得出t-2=2,
(3)点P位于线段EB上,求出PC=t-4,根据PN∥AC,求出PN=16-2t,根据PN=PC,得16-2t=t-4,求出t即可;
(4)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况,①当2<t<4时,求出DP=t-2,PQ=2,AQ=2+t,AM,根据MN∥BC,求出FM=$\frac{1}{2}$t,
再根据S=S梯形AQPD-S△AMF=$\frac{1}{2}$(DP+AQ)•PQ-$\frac{1}{2}$AM•FM代入计算即可;
②当$\frac{20}{3}$<t<8时,求出PC=t-4,AM=12-t,FM=6-$\frac{1}{2}$t,PG=16-2t,再根据S=S梯形AQPG-S△AMF=$\frac{1}{2}$(PG+AC)•PC-$\frac{1}{2}$AM•FM代入计算即可.
解答 解:(1)∵在Rt△ABC中,AC=8cm,BC=4cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,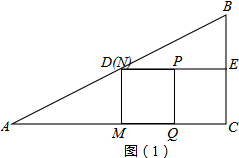
D为AB中点,∴AD=2$\sqrt{5}$,
∴点P在AD段的运动时间为$\frac{2\sqrt{5}}{\sqrt{5}}$=2s.
如图(1)当点P在线段DE上运动时,DP段的运动时间为(t-2)s,
∵DE段运动速度为1cm/s,
∴DP=(t-2)cm,
故答案为:2$\sqrt{5}$,(t-2)cm;
(2)
如图(2)a,此时点D与点N重合,P位于线段DE上.
由三角形中位线定理可知,DM=$\frac{1}{2}$BC=2,
∴DP=DM=2.
由(1)知,DP=t-2,
∴t-2=2,
∴t=4;
(3)如图(2)b,此时点P位于线段EB上.
∵DE=$\frac{1}{2}$AC,AC=8cm,
∴点P在DE段的运动时间为4s,
∴PE=t-6,
∴PB=BE-PE=8-t,PC=PE+CE=t-4.
∵PN∥AC,
∴PN:PB=AC:BC=2,
∴PN=2PB=16-2t.
由PN=PC,得16-2t=t-4,解得t=$\frac{20}{3}$,
所以,当点N落在AB边上时,t=4或t=$\frac{20}{3}$;
故答案为:t=4或t=$\frac{20}{3}$;
(4)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况,如下图所示: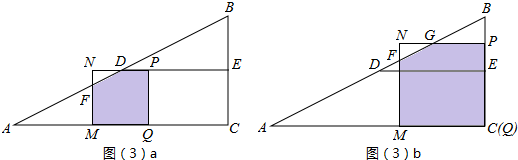
①当2<t<4时,如图(3)a所示.
DP=t-2,PQ=2,∴CQ=PE=DE-DP=4-(t-2)=6-t,AQ=AC-CQ=2+t,AM=AQ-MQ=t.
∵MN∥BC,
∴FM:AM=BC:AC=1:2,
∴FM=$\frac{1}{2}$AM=$\frac{1}{2}$t,
S=S梯形AQPD-S△AMF=$\frac{1}{2}$(DP+AQ)•PQ-$\frac{1}{2}$AM•FM=$\frac{1}{2}$[(t-2)+(2+t)]×2-$\frac{1}{2}$t•$\frac{1}{2}$t=-$\frac{1}{4}$t2+2t;
②当$\frac{20}{3}$<t<8时,如图(3)b所示.
PE=t-6,
∴PC=CM=PE+CE=t-4,AM=AC-CM=12-t,PB=BE-PE=8-t,
∴FM=$\frac{1}{2}$AM=6-$\frac{1}{2}$t,PG=2PB=16-2t,
S=S梯形AQPG-S△AMF=$\frac{1}{2}$(PG+AC)•PC-$\frac{1}{2}$AM•FM=$\frac{1}{2}$[(16-2t)+8]×(t-4)-$\frac{1}{2}$(12-t)•(6-$\frac{1}{2}$t)=-$\frac{5}{4}$t2+22t-84.
∴综上所述,S与t的关系式为:S=$\left\{\begin{array}{l}{-\frac{1}{4}{t}^{2}+2t(2<t<4)}\\{\frac{5}{4}{t}^{2}+22t-84(\frac{20}{3}<t<8)}\end{array}\right.$.
点评 本题考查了相似形综合,是一道运动型综合题,涉及到动点型(两个动点)和动线型,运动过程复杂,难度颇大,对同学们的解题能力要求很高.读懂题意,弄清动点与动线的运动过程,是解题的要点.注意第(2)、(3)问中,分别涉及多种情况,需要进行分类讨论,避免因漏解而失分.


科目:初中数学 来源: 题型:选择题
| A. | 一定有两个相等的实数根 | B. | 一定有实数根 | ||
| C. | 一定有两个不相等的实数根 | D. | 一定没有实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
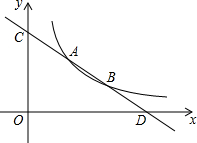 如图,点A(m,m+1),B(m+3,m-1)为第一象限内的点,并且都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,直线AB与y轴交于点C.
如图,点A(m,m+1),B(m+3,m-1)为第一象限内的点,并且都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,直线AB与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com