
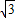 .
.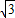 .
.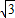 .
.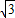 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
A、
| ||
| B、2 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
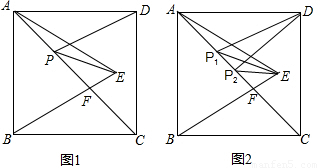
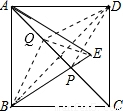
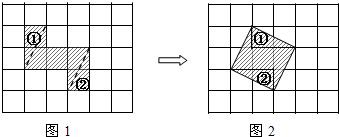
 用“几何画板”中的深度迭代构造“奇妙的勾股树”动态变化,颜色也进行不断改变,在展示数学规律的同时给人一种赏心悦目的感觉.勾股树实际上是通过构造一个直角三角形,并以斜边为边长构造一个正方形(填充颜色),再依次以直角边为边长构造正方形(填充颜色),用参数t控制构造的次数,如:当t=1时,如图1所示,正方形个数为3;当t=2时,如图2所示,正方形个数为7;则当t=5时,正方形的个数为
用“几何画板”中的深度迭代构造“奇妙的勾股树”动态变化,颜色也进行不断改变,在展示数学规律的同时给人一种赏心悦目的感觉.勾股树实际上是通过构造一个直角三角形,并以斜边为边长构造一个正方形(填充颜色),再依次以直角边为边长构造正方形(填充颜色),用参数t控制构造的次数,如:当t=1时,如图1所示,正方形个数为3;当t=2时,如图2所示,正方形个数为7;则当t=5时,正方形的个数为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
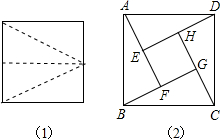 将一个面积为7的正方形分割成如图1所示的四个形状相同、大小相等的直角三角形,再将这四个直角三角形拼成如图2所示的正方形ABCD,其中四边形EFGH也是正方形,求正方形ABCD的面积.
将一个面积为7的正方形分割成如图1所示的四个形状相同、大小相等的直角三角形,再将这四个直角三角形拼成如图2所示的正方形ABCD,其中四边形EFGH也是正方形,求正方形ABCD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com