
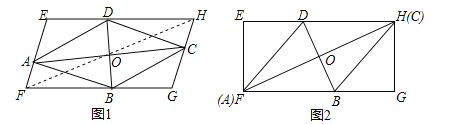
【题目】如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知![]() ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
【答案】(1)证明见解析;(2)矩形EFGH的长为8,宽为4.
【解析】
试题分析:(1)根据菱形的性质可得出OA=OC,OD=OB,再由中点的性质可得出OF=OH,结合对顶角相等即可利用全等三角形的判定定理(SAS)证出△AOF≌△COH,从而得出AF∥CH,同理可得出DH∥BF,依据平行四边形的判定定理即可证出结论;
(2)设矩形EFGH的长为a、宽为b.根据勾股定理及边之间的关系可找出AC=![]() ,BD=
,BD=![]() ,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出
,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出![]() ,套入数据即可得出a=2b①,再根据菱形的面积公式得出
,套入数据即可得出a=2b①,再根据菱形的面积公式得出![]() ②,联立①②解方程组即可得出结论.
②,联立①②解方程组即可得出结论.
试题解析:(1)证明:∵点O是菱形ABCD对角线AC、BD的交点,∴OA=OC,OD=OB,∵点O是线段FH的中点,∴OF=OH.在△AOF和△COH中,∵OA=OC,∠AOF=∠COH,OF=OH,∴△AOF≌△COH(SAS),∴∠AFO=∠CHO,∴AF∥CH.
同理可得:DH∥BF,∴四边形EFGH是平行四边形.
(2)设矩形EFGH的长为a、宽为b,则AC=![]() .
.
∵![]() =2,∴BD=
=2,∴BD=![]() AC=
AC=![]() ,OB=
,OB=![]() BD=
BD=![]() ,OA=
,OA=![]() AC=
AC=![]() .
.
∵四边形ABCD为菱形,∴AC⊥BD,∴∠AOB=90°.
∵四边形EFGH是矩形,∴∠AGH=90°,∴∠AOB=∠AGH=90°,又∵∠BAO=∠CAG,∴△BAO∽△CAG,∴![]() ,即
,即![]() ,解得:a=2b①.
,解得:a=2b①.
∵S菱形ABCD=![]() ACBD=
ACBD=![]()
![]()
![]() =20,∴
=20,∴![]() ②.
②.
联立①②得: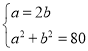 ,解得:
,解得:![]() ,或
,或![]() (舍去),∴矩形EFGH的长为8,宽为4.
(舍去),∴矩形EFGH的长为8,宽为4.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A坐标为(﹣4,4),点B的坐标为(4,0).
(1)求直线AB的解析式;
(2)点M是坐标轴上的一个点,若AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;
(3)如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC﹣OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
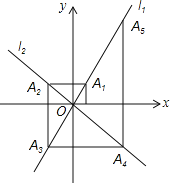
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l2于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( ) 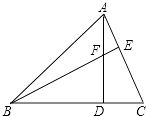
A.40°
B.45°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上老师布置给每个小组一个任务,用抽样调查的方法估计全班同学的平均身高,坐在教室最后面的小强为了争速度,立即就近向他周围的三个同学做调查,计算出他们四个人的平均身高后就举手向老师示意已经完成任务了.小强所选用的这种抽样调查的方式你认为合适吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系式中,正确的是( )
A.(a+b)2=a2﹣2ab+b2
B.(a﹣b)2=a2﹣b2
C.(a+b)2=a2+b2
D.(a+b)(a﹣b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°,②AD∥BC,③PC⊥AB,④四边形ABCD是轴对称图形,其中正确的个数为( ) 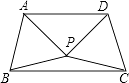
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中适合采用普查的是( )
A. 调查市场上某种白酒中塑化剂的含量 B. 调查鞋厂生产的鞋底能承受的弯折次数
C. 了解某城市居民收看新闻联播的情况 D. 了解某火车的一节车厢内感染禽流感病毒的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com