
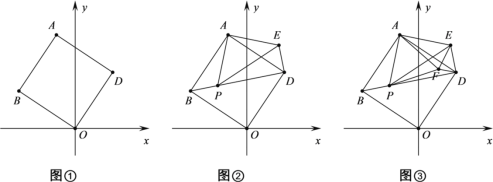
【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.

【答案】(1)点B的坐标为(-3,2);(2)BP与DE的关系是垂直且相等,证明详见解析;(3)∠DFE= 150 °;(4)存在,点N坐标为(![]() +2,1)或(-
+2,1)或(-![]() +2,1)或(
+2,1)或(![]() -3,-1)或(-
-3,-1)或(-![]() -3,-1)或(-1,5)
-3,-1)或(-1,5)
【解析】
(1)如图,过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,证明△BEO≌△OFD,则可得OF=BE,OE=FD,根据点D的坐标(2,3),可求得点B坐标;
(2)如图,通过证明△ABP≌△ADE(SAS),可得∠4=∠5,BP=DE,进而可证明∠BDE=90°,则,BP与DE垂直且相等得证;
(3)由等边△APF和等腰直角△PAE,可知△AFE为等腰三角形,顶角为30°,且EF为底边,所以当腰AF最小时,底边EF则最小,故而AP垂直BD时,AF=AP此时取最小值,此时易证△AFE≌△PFD,故而∠AFE=∠PFD=75°,根据周角为360°,即可计算∠EFD的度数;
(4)分情况讨论,①当BD为菱形的边时,通过作图构造直角三角形,使用勾股定理先求对应点M坐标,再根据菱形的性质及平移思想,求点N坐标;②当BD为菱形的对角线时,M与O重合,此时N与A重合,同样构造直角三角形,使用勾股定理求解即可.
解(1):过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,

∵ABOD为正方形,O是坐标原点,点D的坐标为(2,3),
∴OB=OD,∠BE0=∠DFO,∠BOE=∠ODF,
∴△BEO≌△OFD,
∴OF=BE,OE=FD,
∴点B的坐标为(-3,2),
故答案为:(-3,2);
(2)BP与DE的关系是:垂直且相等;
证明:如图,

∵正方形ABOD,
∴∠BAD=90°,AB=AD,
∵∠PAE=90°,
∴∠BAD-∠3=∠PAE-∠3,
即∠1=∠2,
∵AP=AE,
∴△ABP≌△ADE(SAS),
∴∠4=∠5, BP=DE,
∵∠4+∠6=90°,
∴∠5+∠6=90°,
即∠BDE=90°,
∴BP⊥DE,
∴BP与DE垂直且相等,
故答案为:垂直且相等;
(3)∵△APF为等边三角形,△PAE为等腰直角三角形,且∠PAE=90°,
∴AF=AE,∠FAE=30°,
即△AFE为等腰三角形,且EF为底边,
∴当EF最小时,AF=AE应该取最小值,即AP应当取最小值,
∵四边形ABOD为矩形,BD为ABOD一条对角线,
∴当AP⊥BD时,EF有最小值,如下图所示,

∴AP=PD=AE,∠PAD=∠APD=90°,
∴∠EAF=∠DPF=30°,
又∵AF=PF,
∴△AFE≌△PFE,
∴∠PFD=∠AFE=75°,
∴∠EFD=360°-75°-75°-60°=150°,
即,当EF取最小值时,∠DFE=150°,
故答案为:150;
(4)∵D(2,3),
∴OD=![]() ,
,
∴BD=![]() ,
,
①当BD为菱形的边时,
(Ⅰ)如图,作BQ⊥x轴于Q,

MB=BD=![]() ,在Rt△BQM中根据勾股定理,可得M1(
,在Rt△BQM中根据勾股定理,可得M1(![]() -3,0)、M2(-
-3,0)、M2(-![]() -3,0),
-3,0),
∵B向右平移5个单位再向上平移1个单位得到D,
∴N1(![]() +2,1)、N2(-
+2,1)、N2(-![]() +2,1);
+2,1);
(Ⅱ)如图,作TP垂直x轴于P,

MD=BD=![]() ,在Rt△DPM中根据勾股定理,可得M3(
,在Rt△DPM中根据勾股定理,可得M3(![]() +2,0)、M4(-
+2,0)、M4(-![]() +2,0),
+2,0),
∵D向左平移5个单位再向下平移1个单位得到B,
∴N3(![]() -3,-1)、N4(-
-3,-1)、N4(-![]() -3,-1)
-3,-1)
②当BD为菱形的对角线时,M与O重合,此时N与A重合,
如图,作AJ∥x轴交y轴于R,过点D作JK⊥x轴垂足为K,交AJ于点J,

易证△ALD≌△DKO,
∴JK=5,
在Rt△ARO中使用勾股定理,即可求N5(-1,5),
综上所述,点N坐标为(![]() +2,1)或(-
+2,1)或(-![]() +2,1)或(
+2,1)或(![]() -3,-1)或(-
-3,-1)或(-![]() -3,-1)或(-1,5).
-3,-1)或(-1,5).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )

A.![]() B.
B.![]()
C.![]() D.﹣2≤k≤2且k≠0
D.﹣2≤k≤2且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校对学生暑假参加志愿服务的时间进行抽样调查,将收集的数据分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组进行整理,并绘制成如下的统计图表(图中信息不完整).
五组进行整理,并绘制成如下的统计图表(图中信息不完整).

分组统计表
组别 | 志愿服务时间 | 人数 |
A |
|
|
B |
| 40 |
C |
|
|
D |
|
|
E |
| 16 |
请结合以上信息解答下列问题
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)补全“人数分组统计图①中![]() 组的人数和图②
组的人数和图②![]() 组和
组和![]() 组的比例值”;
组的比例值”;
(3)若全校学生人数为800人,请估计全校参加志愿服务时间在![]() 的范围的学生人数.
的范围的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
(1)AC⊥BD;
(2)四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com