
【题目】已知![]() 是
是![]() 上一点,
上一点,![]() .
.
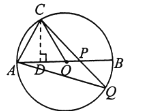
(Ⅰ)如图①,过点![]() 作
作![]() 的切线,与
的切线,与![]() 的延长线交于点
的延长线交于点![]() ,求
,求![]() 的大小及
的大小及![]() 的长;
的长;

(Ⅱ)如图②,![]() 为
为![]() 上一点,
上一点,![]() 延长线与
延长线与![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的大小及
的大小及![]() 的长.
的长.
【答案】(Ⅰ)![]() ,PA=4;(Ⅱ)
,PA=4;(Ⅱ)![]() ,
,![]()
【解析】
(Ⅰ)易得△OAC是等边三角形即∠AOC=60°,又由PC是○O的切线故PC⊥OC,即∠OCP=90°可得∠P的度数,由OC=4可得PA的长度
(Ⅱ)由(Ⅰ)知△OAC是等边三角形,易得∠APC=45°;过点C作CD⊥AB于点D,易得AD=![]() AO=
AO=![]() CO,在Rt△DOC中易得CD的长,即可求解
CO,在Rt△DOC中易得CD的长,即可求解
解:(Ⅰ)∵AB是○O的直径,∴OA是○O的半径.
∵∠OAC=60°,OA=OC,∴△OAC是等边三角形.
∴∠AOC=60°.
∵PC是○O的切线,OC为○O的半径,
∴PC⊥OC,即∠OCP=90°∴∠P=30°.
∴PO=2CO=8.
∴PA=PO-AO=PO-CO=4.
(Ⅱ)由(Ⅰ)知△OAC是等边三角形,
∴∠AOC=∠ACO=∠OAC=60°∴∠AQC=30°.
∵AQ=CQ,∴∠ACQ=∠QAC=75°
∴∠ACQ-∠ACO=∠QAC-∠OAC=15°即∠QCO=∠QAO=15°.
∴∠APC=∠AQC+∠QAO=45°.
如图②,过点C作CD⊥AB于点D.
∵△OAC是等边三角形,CD⊥AB于点D,
∴∠DCO=30°,AD=![]() AO=
AO=![]() CO=2.
CO=2.
∵∠APC=45°,∴∠DCQ=∠APC=45°
∴PD=CD
在Rt△DOC中,OC=4,∠DCO=30°,∴OD=2,∴CD=2![]()
∴PD=CD=2![]()
∴AP=AD+DP=2+2![]()


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】如图,点C是半圆O上的一点,AB是⊙O的直径,D是![]() 的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
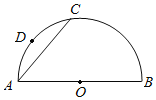
下面是小明的做法,请帮他补充完整(包括补全图形)
解:补全半圆O为完整的⊙O,连接AD,延长DE交⊙O于点H(补全图形)
∵D是![]() 的中点,
的中点,
∴![]() .
.
∵DE⊥AB,AB是⊙O的直径,
∴![]() ( )(填推理依据)
( )(填推理依据)
∴![]()
∴∠ADF=∠FAD( )(填推理依据)
∴AF=DF( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() .
.
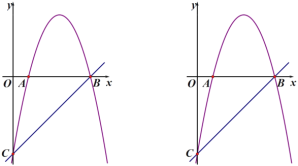
(1)求抛物线的函数表达式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一动点,求
上方抛物线上的一动点,求![]() 面积
面积![]() 的最大值并求出此时点
的最大值并求出此时点![]() 的坐标;
的坐标;
(3)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,连接
,连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的一个夹角等于
的一个夹角等于![]() 的3倍时,请直接写出点
的3倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列人第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上![]() 处垂直于地面竖立了高度为
处垂直于地面竖立了高度为![]() 米的标杆
米的标杆![]() ,这时地面上的点
,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上,测得
正好在同一直线上,测得![]() 米,将标杆向后平移到点
米,将标杆向后平移到点![]() 处,这时地面上的点
处,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上(点
正好在同一直线上(点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 与古塔底处的点
与古塔底处的点![]() 在同一直线上) ,这时测得
在同一直线上) ,这时测得![]() 米,
米,![]() 米,请你根据以上数据,计算古塔的高度
米,请你根据以上数据,计算古塔的高度![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
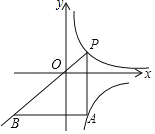
A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
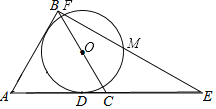
【题目】如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
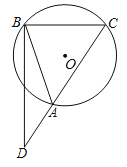
【题目】如图,⊙O的半径为2,弦AB的长为2![]() ,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形MNPQ中,动点R从点N出发,沿着N-P-Q-M方向移动至M停止,设R移动路程为x,MNR面积为y,那么y与x的关系如图②,下列说法不正确的是( )

A.当x=2时,y=5B.矩形MNPQ周长是18
C.当x=6时,y=10D.当y=8时,x=10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com