
分析 (1)根据调配方案,即可解决问题.
(2)根据每台的运费即可得出函数关系式;利用不等式求出自变量的取值范围.
(3)列出不等式,求整数解,利用一次函数的性质确定最小值.
解答 解:(1)甲地运往B市的设备有(17-x)台,
乙地运往A市的设备有(18-x)台,
乙地运往B市的设备有15-(18-x)=(x-3)台,
(2)根据题意得:y=800x+500(17-x)+700(18-x)+600(x-3),
即y=200x+19300.
由$\left\{\begin{array}{l}x≥0\\ 17-x≥0\\ 18-x≥0\\ x-3≥0\end{array}\right.$,解得3≤x≤17.
∴自变量的取值范围是:x为正整数且3≤x≤17.
(3)∵要使总运费不高于20200元,
∴200x+19300≤20200,
解得:x≤4.5.(8分)
又∵x为正整数且3≤x≤17,
∴x=3或4.
∴该公司调配方案有两种:
方案一:甲地运往A市3台,运往B市14台,乙地运往A市15台,运往B市0台;
方案二:甲地运往A市4台,运往B市13台,乙地运往A市14台,运往B市1台;
∵在y=200x+19300中,k=200>0,
∴y随x的增大而增大,
∴当x=3时,总运费最小,最小值是y=200×3+19300=19900(元).
即甲地运往A市3台,运往B市14台,乙地运往A市15台,运往B市0台总运费最小,最小值是19900元.
点评 此题主要考查了一次函数的应用以及不等式的解法和一次函数的最值问题,根据题意用x表示出运往各地的台数是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
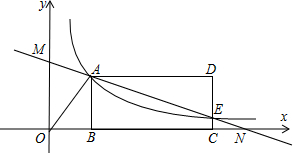 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
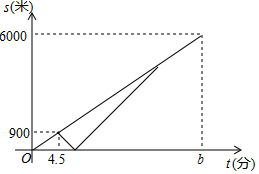 周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com