练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，问直线EF与AB有怎样的位置关系？为什么？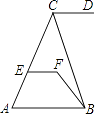

    【答案】解：平行． 证明：∵CD∥AB，
    ∴∠ABC=∠DCB=70°；
    又∵∠CBF=20°，
    ∴∠ABF=∠ABC﹣∠CBF=70°﹣20°=50°；
    ∴∠ABF+∠EFB=50°+130°=180°；
    ∴EF∥AB（同旁内角互补，两直线平行）
    【解析】两直线的位置关系有两种：平行和相交，根据图形可以猜想两直线平行，然后根据条件探求平行的判定条件．
    【考点精析】根据题目的已知条件，利用平行线的判定与性质的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

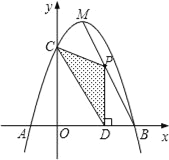
    【题目】如图，抛物线y=﹣x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为B（3，0）．C（0，3），点M是抛物线的顶点．

    （1）求二次函数的关系式；

    （2）点P为线段MB上一个动点，过点P作PD⊥x轴于点D．若OD=m，△PCD的面积为S，试判断S有最大值或最小值？并说明理由；

    （3）在MB上是否存在点P，使△PCD为直角三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠1=∠2．∠GFA=55°，∠ACB=75°，AQ平分∠FAC，AH∥BD，求∠HAQ的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若⊙O的半径为5，点A到圆心O的距离为4，则点A在⊙O______(填“内”、“上”或“外”)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平移、旋转和轴对称这些图形变换下，它们共同具有的特征是（　　）

    A. 图形的形状、大小没有改变，对应线段平行且相等

    B. 图形的形状、大小没有改变，对应线段垂直，对应角相等

    C. 图形的形状、大小都发生了改变，对应线段相等，对应角相等

    D. 图形的形状、大小没有改变，对应线段相等，对应角相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三角形中的角平分线的性质与一个角的平分线性质相同.如题:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.请你结合条件认真研究,然后写出三个正确的结论.

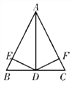
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算(﹣x5)7+(﹣x7)5的结果是(　　)

    A. ﹣2x12B. ﹣2x35C. ﹣2x70D. 0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】长春南溪湿地公园总占地面积约为3 100 000平方米．3 100 000这个数用科学记数法表示为（　　）

    A. 3.1×105 B. 3.1×106 C. O.31×107 D. 3.1×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：-2xy2·(-3xy) 2 =__________.

    查看答案和解析>>

    同步练习册答案