
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
【答案】(1)-34(2)2345
【解析】
(1)最大的数字为9,所以最大的两位“相连数”是89,最小的三位“相连数”,百位数最小,即该相连数最小,即百位数为1,所以是123,符合题意,然后列式计算求差;
(2)由定义得个位数最大为9,9×469=4221,则这个“相连数“最大为四位数,最小为三位数,设个位数为x,十位数为10(x-1),百位数为100(x-2),千位数为1000(x-3),相加即为此“相连数“=469x.列方程求解即可.
(1)最大的两位“相连数”是89,最小的三位“相连数”是123,
则89﹣123=﹣34;
(2)设这个“相连数”个位数字为x,
若这个“相连数”为4位数,则其个位数字最大为9,
根据题意得:1000(x﹣3)+100(x﹣2)+10(x﹣1)+x=469x,
解得x=5,
则该“相连数“为2345:
这个“相连数”为3位数,
根据题意得:100(x﹣2)+10(x﹣1)+x=469x,
解得:x=﹣![]() ,不符合题意;
,不符合题意;
则这个“相连数”为2345,


科目:初中数学 来源: 题型:
【题目】如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
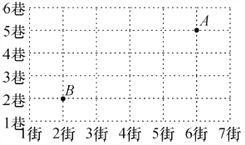
A. (2,2)→(2,5)→(5,6) B. (2,2)→(2,5)→(6,5)
C. (2,2)→(6,2)→(6,5) D. (2,2)→(2,3)→(6,3)→(6,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
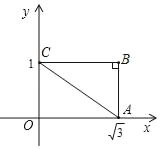
【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(![]() ,0),C(0,1).
,0),C(0,1).
(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试验与探究:我们知道分数![]() 写为小数即
写为小数即![]() ,反之,无限循环小数
,反之,无限循环小数![]() 写成分数即
写成分数即![]() .一般地,任何一个无限循环小数都可以写成分数形式.现在就以
.一般地,任何一个无限循环小数都可以写成分数形式.现在就以![]() 为例进行讨论:设
为例进行讨论:设![]() =x,由
=x,由![]() =0.7777…,可知,10x﹣x=7.77…﹣0.777…=7,即10x﹣x=7,解方程得
=0.7777…,可知,10x﹣x=7.77…﹣0.777…=7,即10x﹣x=7,解方程得![]() ,于是得
,于是得![]() =
=![]() .
.
请仿照上述例题完成下列各题:
(1)请你把无限循环小数![]() 写成分数,即
写成分数,即![]() =_____.
=_____.
(2)你能化无限循环小数![]() 为分数吗?请仿照上述例子求解之.
为分数吗?请仿照上述例子求解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
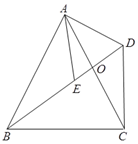
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
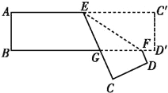
(1)∠C′EF=32°;(2)∠AEC=148°;(3)∠BGE=64°;(4)∠BFD=116°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
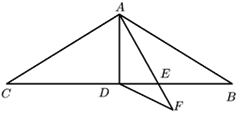
【题目】已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:
(1)△ABD≌△CFD;
(2)BE⊥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点E,则DF的长为( )
A. 4.5 B. 5 C. 5.5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com