
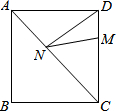
 正方形ABCD的边长为12,M在DC上,DM=3,N是AC上的一动点,则DN+MN的最小值是15.
正方形ABCD的边长为12,M在DC上,DM=3,N是AC上的一动点,则DN+MN的最小值是15. 分析 由正方形的性质可知点B与点D关于AC对称,从而可得到NB=DN,从而得到DN+MN=BN+MN,根据两点之间线段最短可知当B、N、M在一条直线上时,DN+MN有最小值,最后利用勾股定理求得BM的长即可.
解答 解:如图所示:连接BN.
∵四边形ABCD为正方形,
∴点B与点D关于AC对称.
∴NB=DN.
∴DN+MN=BN+MN.
由两点之间线段可知:当B、N、M在一条直线上时,DN+MN有最小值.
在Rt△BMC中由勾股定理得:MB=$\sqrt{B{C}^{2}+M{C}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15.
∴DN+MN的最小值为15.
故答案为:15.
点评 本题主要考查的是正方形的性质、轴对称图形的性质、勾股定理的应用,明确当B、N、M在一条直线上时,DN+MN有最小值是解题的关键.


科目:初中数学 来源: 题型:解答题
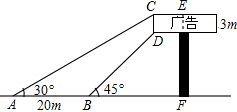 如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).
如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
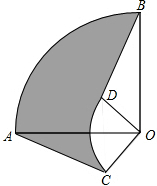 如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.
如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
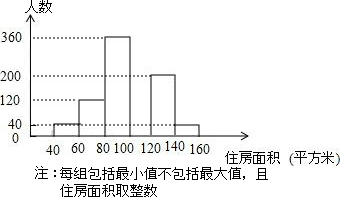 2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:
2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:| 年收入(万元) | 1.2 | 1.8 | 3 | 5 | 10 |
| 被调查的消费者人数(人) | 200 | 500 | 200 | 70 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com