
如图, 为正方形
为正方形 对角线AC上一点,以
对角线AC上一点,以 为圆心,
为圆心,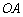 长为半径的⊙
长为半径的⊙ 与
与 相切于点
相切于点 .
.
(1)求证: 与⊙
与⊙ 相切;
相切;
(2)若⊙ 的半径为1,求正方形
的半径为1,求正方形 的边长.
的边长.
 |

科目:初中数学 来源: 题型:
如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则( )
,则( )
A.点 一定在射线
一定在射线 上 B.点
上 B.点 一定在线段
一定在线段 上
上
C.点 可以在射线
可以在射线 上 ,也可以在线段
上 ,也可以在线段 上 D.点
上 D.点 可以在射线
可以在射线 上 ,也可以在线段
上 ,也可以在线段

查看答案和解析>>
科目:初中数学 来源: 题型:
某射击运动员在相同条件下的射击160次,其成绩记录如下:
| 射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| 射中9环以上的次数 | 15 | 33 | 63 | 79 | 97 | 111 | 130 | |
| 射中9环以上的频率 | 0.75 | 0.83 | 0.80 | 0.79 | 0.79 | 0.79 | 0.81 |
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0 .1),并简述理由.
.1),并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙O交AB于点D,取AC的中点E,连结DE、OE.(1)求证:DE是⊙O的切线;(2)如果⊙O的半径是1.5cm,ED=2cm,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com