
【题目】在平面直角坐标系中,等边![]()
![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,点
,点![]() ,点
,点![]() 在第一象限.
在第一象限.
(1)若抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() ,求抛物线
,求抛物线![]() 的表达式.
的表达式.
(2)点![]() 是平面内一点,以点
是平面内一点,以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,现将抛物线
为顶点的四边形是平行四边形,现将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ,若抛物线
,若抛物线![]() 经过
经过![]() 、
、![]() 两点,求抛物线
两点,求抛物线![]() 的表达式.
的表达式.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]()
【解析】
(1)根据题意可求出点B坐标,已知O,A,B的坐标利用待定系数法可以求出抛物线![]() 的表达式;
的表达式;
(2)抛物线![]() 是由
是由![]() 平移得到的,所以两条抛物线的a值不变,点
平移得到的,所以两条抛物线的a值不变,点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点组成平行四边形,数形结合找出D点坐标,通过待定系数法求出抛物线
为顶点组成平行四边形,数形结合找出D点坐标,通过待定系数法求出抛物线![]() 的表达式.
的表达式.
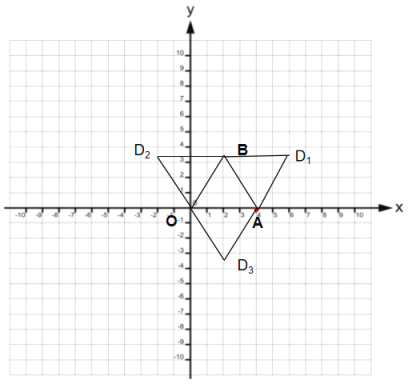
解:(1)∵△AOB是等边三角形,点![]() ,点
,点![]() ,点
,点![]() 在第一象限
在第一象限
∴点B坐标为(2,2![]() )
)
设抛物线![]() 的表达式为y=ax2+bx+c,将
的表达式为y=ax2+bx+c,将![]() ,
,![]() ,B(2,2
,B(2,2![]() )代入,得
)代入,得
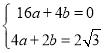
解得 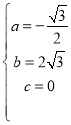
∴抛物线![]() 的表达式为
的表达式为![]() .
.
(2)∵以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
由图可知点D有3种情况. ![]() ,
,![]() ,
,![]()
∵抛物线![]() 是由
是由![]() 平移得到的
平移得到的
∴抛物线![]() 的a值为
的a值为![]()
设抛物线![]() 的关系式为y=
的关系式为y=![]() x2+bx+c
x2+bx+c
①当![]() 时,将
时,将![]() ,
,![]() 代入,得
代入,得
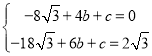
解得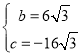
∴抛物线![]() 的关系式为y=
的关系式为y=![]() x2+6
x2+6![]() x-16
x-16![]() .
.
②当![]() 时,将
时,将![]() ,
,![]() 代入,得
代入,得
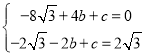
解得
∴抛物线![]() 的关系式为y=
的关系式为y=![]() x2+
x2+![]() x+
x+![]() .
.
③当![]() 时,将
时,将![]() ,
,![]() 代入,得
代入,得
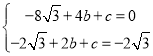
解得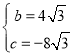
∴抛物线![]() 的关系式为y=
的关系式为y=![]() x2+4
x2+4![]() x-8
x-8![]() .
.
综上,抛物线![]() 的关系式为
的关系式为![]() ,
,![]() ,
,![]() .
.
故答案为(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]()


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将一矩形OABC放在平面直角坐标系中,O为原点,点B、C分别在x轴、y轴上,点A(4,3),点D为线段OC上一动点,将△BOD沿BD翻折,点O落在点E处,连接CE,则CE的最小值为______.
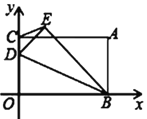
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
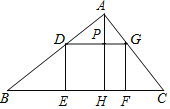
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车经销商为了能更好的了解某季度纯电动汽车的续航能力,现分两次不重复的各抽取了10台纯电动车进行了续航里程的测试.并将测试的情况进行整理、描述和分析(续航里程用x表示,共分成四组:(A)100≤x<200,(B)200≤x<300,(C)300≤x<400,(D)x≥400,单位:km).下面给出了部分信息:
第一次抽取10台车的续航里程在C组中的数据是:380,310,300,310.
第二次抽取10台车的续航里程是:220,301,175,310,400,310,385,430,234,455.
第一次测试的续航里程扇形统计图如图
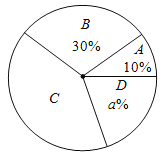
两次测试的续航里程统计表
第一次 | 第二次 | |
平均里程 | 321.4 | b |
中位数 | c | 310 |
众数 | 310 | 310 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值,a= ,b= ,c .
(2)根据以上数据,你认为这两次测试中的哪一次的纯电动汽车续航能力更强?请说明理由(一条理由即可).
(3)若经销商这一季度共购进1600台纯电动汽车,结合这两次测试,估计这一季度续航能力较强(x≥380)的纯电动汽车有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机取出一个小球,记下数字为
,小红在剩下的3个小球中随机取出一个小球,记下数字为![]() 。
。
(1)计算由![]() 、
、![]() 确定的点
确定的点![]() 在函数
在函数![]() 的图象上的概率;
的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若![]() 、
、![]() 满足
满足![]() >6则小明胜,若
>6则小明胜,若![]() 、
、![]() 满足
满足![]() <6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
<6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,![]() ),则点C的坐标是( )
),则点C的坐标是( )
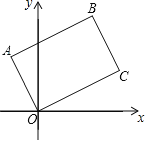
A. (4,2)B. (2,4)C. (![]() ,3)D. (3,
,3)D. (3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种火爆的网红电子产品,每件产品成本![]() 元、工厂将该产品进行网络批发,批发单价
元、工厂将该产品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.
![]() 直接写出
直接写出![]() 与
与![]() 之间所满足的函数关系式,并写出自变量
之间所满足的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 若一次性批发量不超过
若一次性批发量不超过![]() 件,当批发量为多少件时,工厂获利最大?最大利润是多少?
件,当批发量为多少件时,工厂获利最大?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com