

| A. | 5 | B. | 7 | C. | 8 | D. | $\frac{13}{2}$ |
分析 作CH⊥AB于H,如图,根据菱形的性质可判断△ABC为等边三角形,则CH=$\frac{\sqrt{3}}{2}$AB=4$\sqrt{3}$,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
解答 解:作CH⊥AB于H,如图,
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH=$\frac{\sqrt{3}}{2}$AB=4$\sqrt{3}$,AH=BH=4,
∵PB=3,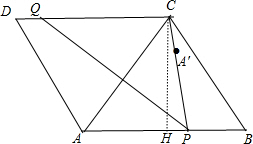
∴HP=1,
在Rt△CHP中,CP=$\sqrt{(4\sqrt{3})^{2}+{1}^{2}}$=7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,
而CD∥AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故选B.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了折叠的性质.解决本题的关键是确定A′在PC上时CA′的长度最小.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )| A. | (x+1)(x+2)=18 | B. | x2-3x+16=0 | C. | (x-1)(x-2)=18 | D. | x2+3x+16=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,对称轴为直线x=$\frac{7}{2}$的抛物线经过点A(6,0)和B(0,-4).
如图,对称轴为直线x=$\frac{7}{2}$的抛物线经过点A(6,0)和B(0,-4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.8×103 | B. | 28×103 | C. | 2.8×104 | D. | 0.28×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com