
如图,已知AB是⊙O的直径,AB=8, 点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,联结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.
(1)若![]() =
=![]() ,求∠F的度数;
,求∠F的度数;
(2)设![]() 写出
写出![]() 与
与![]() 之间的函数解析式,并写出定义域;
之间的函数解析式,并写出定义域;
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.
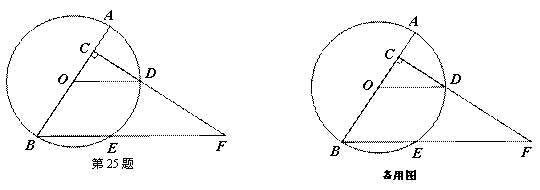
(1)联结OE-
∵![]() =
=![]() ∴∠BOE=∠EOD--
∴∠BOE=∠EOD--
∵OD//BF ∴∠DOE=∠BEO
∵OB=OE ∴∠OBE=∠OEB-
∴∠OBE=∠OEB=∠BOE=60°
∵∠FCB=90°∴ ∠F=30°
∴ ![]()
∵OD//BF ∴ ![]() -
-
∴![]() ∴
∴ ![]()
(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB
∴ ∠COD=∠DOE, ∴C关于直线OD的对称点为P在线段OE上-
若△PBE为等腰三角形
① 当PB=PE,不合题意舍去;当EB=EP ![]() -
-
② 当BE=BP 作BM⊥OE,垂足为M,
易证△BEM∽△DOC∴![]() ∴
∴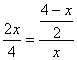
整理得: ![]() (负数舍去)分)
(负数舍去)分)
综上所述:当OC的长为![]() 或
或![]() 时,△PBE为等腰三角形。
时,△PBE为等腰三角形。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.| BE | AD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com