
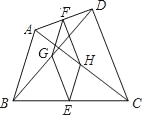
【题目】如图,四边形ABCD中,AB=CD,点E、F、G、H分别是BC、AD、BD、AC的中点,猜想四边形EHFG的形状并说明理由.

【答案】证明见解析
【解析】
首先运用三角形中位线定理可得到FG∥AB,HE∥AB,FH∥CD,GE∥DC,从而在根据平行于同一条直线的两直线平行得到GE∥FH,GF∥EH,可得到四边形GFHE是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.
∵四边形ABCD中,点E、F、G、H分别是BC、AD、BD、AC的中点,
∴FG∥AB,HE∥AB,FH∥CD,GE∥DC,
∴GE∥FH,GF∥EH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形,
∵四边形ABCD中,点E、F、G、H分别是BC、AD、BD、AC的中点,
∴FG是△ABD的中位线,GE是△BCD的中位线,
∴GF=![]() AB,GE=
AB,GE=![]() CD,
CD,
∵AB=CD,
∴GF=GE,
∴四边形EHFG是菱形.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为4,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S10的值为 . 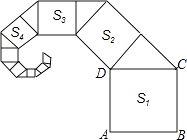
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )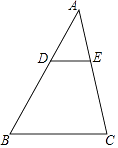
A.4
B.8
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年两会提出:随着城镇化水平的提高,为了房地产去库存,国家鼓励农民进城买房,可享受政府担保免收利息的惠民政策,小王家购买了一套学区房,首付15万元后,剩余部分贷款,贷款金额按月分期还款,每月还款数相同,计划每月还款y万元,x个月还清贷款,已知y是x的反比例函数,其图象如图所示.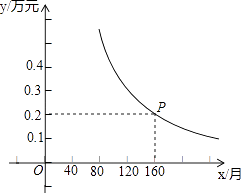
(1)求y与x的函数解析式(关系式),并求小王家购买的学区房的总价是多少万元?
(2)若计划80个月还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )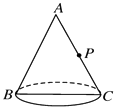
A.3 ![]() cm
cm
B.3 ![]() cm
cm
C.9cm
D.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC中∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠DAC=22.5°,其中正确的是( )

A. ①②④B. ③④⑤C. ①③④D. ①②⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com