
【题目】如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是![]() 的中点,连接CE、CF、BP.
的中点,连接CE、CF、BP.
(1)求证:AB是⊙O的切线.
(2)若OA=4,则
①当![]() 长为_____时,四边形OECF是菱形;
长为_____时,四边形OECF是菱形;
②当![]() 长为_____时,四边形OCBP是正方形.
长为_____时,四边形OCBP是正方形.![]()

【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)证明垂直就可以证明是切线.(2)利用四边形OECF是菱形的性质反推可得到DP长.利用正方形OECF的性质反推可得到DP长.
解:(1)∵在△ABO中,OA=OB,C是AB的中点,
∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
(2)①∵OECF为菱形,
∴OE=EC,∠EOC=∠COF.
∴OE=EC=OC.
∴∠EOC=∠COF=60°.
∴∠DOF=60°.
又∵P为弧DF的中点,
∴∠DOP=30°.
∵∠AOC=60°,∠OCA=90°,
∴OC=![]() OA=2.
OA=2.
∴弧DP的长=![]() .
.
②∵四边形OCBP为正方形,
∴∠COB=∠POB=45°.
∴OC=![]() OB=2
OB=2![]() .
.
∵P为弧DF的中点,
∴∠DOP=45°.
∴弧DP的长=![]() .
.
故答案为:①![]() ;②
;②![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,D 为∠BAC 的外角平分线上一点并且满足 BD=CD, 过 D 作 DE⊥AC 于 E,DF⊥AB 交 BA 的延长线于 F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
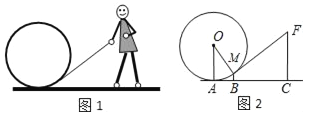
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com