
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
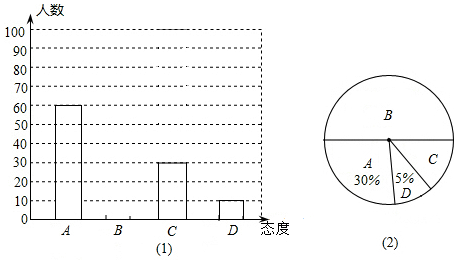
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检查一枚用于发射卫星的运载火箭的各零部件 | |
| B. | 了解一批圆珠笔的寿命 | |
| C. | 考察人们保护海洋的意识 | |
| D. | 了解全国九年级学生身高的现状 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
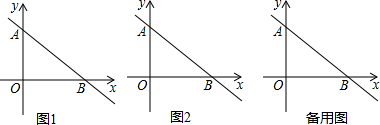
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com