
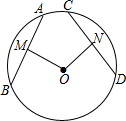
 小雅同学在学习圆的基本性质时发现了一个结论:如图,在⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.
小雅同学在学习圆的基本性质时发现了一个结论:如图,在⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.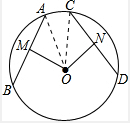 解:(1)连结OA,OC,
解:(1)连结OA,OC, AB,CN=
AB,CN= CD,在Rt△AOM中,AM=
CD,在Rt△AOM中,AM=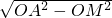 ,在Rt△CON中,CN=
,在Rt△CON中,CN= ,
,
 AB,CN=
AB,CN= CD,再利用勾股定理得到AM=
CD,再利用勾股定理得到AM=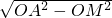 ,CN=
,CN= ,又OA=OC,OM=ON即可得到结论;
,又OA=OC,OM=ON即可得到结论;

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
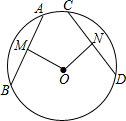 小雅同学在学习圆的基本性质时发现了一个结论:如图,在⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.
小雅同学在学习圆的基本性质时发现了一个结论:如图,在⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•武汉模拟)小雅同学在学习圆的基本性质时发现了一个结论:如图,⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.
(2011•武汉模拟)小雅同学在学习圆的基本性质时发现了一个结论:如图,⊙O中,OM⊥弦AB于点M,ON⊥弦CD于点N,若OM=ON,则AB=CD.查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省武汉市部分学校九年级(上)期末数学试卷(解析版) 题型:解答题
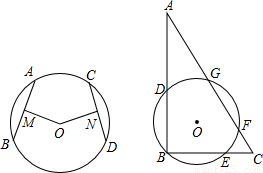
查看答案和解析>>
科目:初中数学 来源:2012年湖北省武汉市元月调考九年级数学试卷(解析版) 题型:解答题
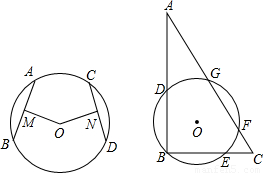
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com