
ΓΨΧβΡΩΓΩ»γΆΦΘ®1Θ©Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ¥ΙΉψΈΣAΘ§BΘ§
¥ΙΉψΈΣAΘ§BΘ§![]() Θ§Βψ
Θ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ“‘ΟΩΟκ2
…œ“‘ΟΩΟκ2![]() ΒΡΥΌΕ»”…Βψ
ΒΡΥΌΕ»”…Βψ![]() œρΒψ
œρΒψ![]() ‘ΥΕ·Θ§Ά§ ±Βψ
‘ΥΕ·Θ§Ά§ ±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ”…Βψ
…œ”…Βψ![]() œρΒψ
œρΒψ![]() ‘ΥΕ·Θ°ΥϋΟ«‘ΥΕ·ΒΡ ±ΦδΈΣ
‘ΥΕ·Θ°ΥϋΟ«‘ΥΕ·ΒΡ ±ΦδΈΣ![]() Θ®
Θ®![]() Θ©Θ°
Θ©Θ°
Θ®1Θ©![]() ΓΓΓΓΓΓΓΓ
ΓΓΓΓΓΓΓΓ ![]() Θ§
Θ§![]() ΓΓΓΓΓΓΓΓ
ΓΓΓΓΓΓΓΓ ![]() ΘΜΘ®”Ο
ΘΜΘ®”Ο![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
Θ®2Θ©»γΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ
ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§Β±
ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§Β±![]() ±Θ§
±Θ§![]() ”κ
”κ![]() «Ζώ»ΪΒ»Θ§≤Δ≈–Εœ¥Υ ±œΏΕΈ
«Ζώ»ΪΒ»Θ§≤Δ≈–Εœ¥Υ ±œΏΕΈ![]() ΚΆœΏΕΈ
ΚΆœΏΕΈ![]() ΒΡΈΜ÷ΟΙΊœΒΘ§«κΖ÷±πΥΒΟςάμ”…ΘΜ
ΒΡΈΜ÷ΟΙΊœΒΘ§«κΖ÷±πΥΒΟςάμ”…ΘΜ
Θ®3Θ©»γΆΦΘ®2Θ©Θ§ΫΪΆΦΘ®1Θ©÷–ΒΡΓΑ![]() Θ§
Θ§![]() Γ±Θ§ΗΡΈΣΓΑ
Γ±Θ§ΗΡΈΣΓΑ![]() Γ±Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ°…ηΒψ
Γ±Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ°…ηΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»ΈΣ
ΒΡ‘ΥΕ·ΥΌΕ»ΈΣ![]()
![]() Θ§ «Ζώ¥φ‘Ύ”–άμ ΐ
Θ§ «Ζώ¥φ‘Ύ”–άμ ΐ![]() Θ§
Θ§![]() ”κ
”κ![]() «Ζώ»ΪΒ»ΘΩ»τ¥φ‘ΎΘ§«σ≥ωœύ”ΠΒΡxΓΔtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
«Ζώ»ΪΒ»ΘΩ»τ¥φ‘ΎΘ§«σ≥ωœύ”ΠΒΡxΓΔtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
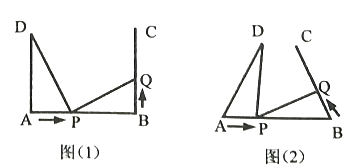
ΓΨ¥πΑΗΓΩΘ®1Θ©2tΘ§8-2tΘΜΘ®2Θ©ΓςADP”κΓςBPQ»ΪΒ»Θ§œΏΕΈPD”κœΏΕΈPQ¥Ι÷±Θ§άμ”…ΦϊΫβΈωΘΜΘ®3Θ©¥φ‘Ύ![]() Μρ
Μρ![]() Θ§ ΙΒΟΓςADP”κΓςBPQ»ΪΒ»Θ°
Θ§ ΙΒΟΓςADP”κΓςBPQ»ΪΒ»Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“β÷±Ϋ”Ω…ΒΟ¥πΑΗ.
Θ®2Θ©”…t=1Ω…ΒΟΓςACPΚΆΓςBPQ÷–Ης±ΏΒΡ≥ΛΘ§”…SASΆΤ≥ωΓςACPΓ’ΓςBPQΘ§ΫχΕχΗυΨί»ΪΒ»»ΐΫ«–Έ–‘÷ ΒΟΓœAPC+ΓœBPQ=90ΓψΘ§Ψί¥Υ≈–ΕœœΏΕΈPCΚΆPQΒΡΈΜ÷ΟΙΊœΒΘΜ
Θ®3Θ©ΦΌ…ηΓςACPΓ’ΓςBPQΘ§”ΟtΚΆx±μ Ψ≥ω±Ώ≥ΛΘ§ΗυΨίΕ‘”Π±ΏœύΒ»Ϋβ≥ωtΚΆxΒΡ÷ΒΘΜ
‘ΌΦΌ…ηΓςACPΓ’ΓςBQPΘ§”Ο…œ≤ΫΒΡΖΫΖ®«σΫβΘ§ΉΔ“β¥Υ ±ΒΡΕ‘”Π±ΏΚΆ…œ≤Ϋ≤Μ“Μ―υ.
Θ®1Θ©”…Χβ“βΒΟΘΚ![]() 2tΘ§
2tȧ![]() 8-2tȰ
8-2tΘ°
Θ®2Θ©ΓςADP”κΓςBPQ»ΪΒ»Θ§œΏΕΈPD”κœΏΕΈPQ¥Ι÷±Θ°
άμ”…»γœ¬ΘΚ
Β±t=1 ±Θ§AP=BQ=2Θ§BP=AD=6Θ§
”÷ΓœA=ΓœB=90ΓψΘ§
‘ΎΓςADPΚΆΓςBPQ÷–Θ§
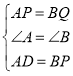 Θ§ΓύΓςADP
Θ§ΓύΓςADP![]() ΓςBPQΘ®SASΘ©Θ§ΓύΓœADP=ΓœBPQΘ§ΓύΓœAPD+ΓœBPQ=ΓœAPD+ΓœADP=90ΓψΘ§ΓύΓœDPQ=90ΓψΘ§Φ¥œΏΕΈPD”κœΏΕΈPQ¥Ι÷±Θ°
ΓςBPQΘ®SASΘ©Θ§ΓύΓœADP=ΓœBPQΘ§ΓύΓœAPD+ΓœBPQ=ΓœAPD+ΓœADP=90ΓψΘ§ΓύΓœDPQ=90ΓψΘ§Φ¥œΏΕΈPD”κœΏΕΈPQ¥Ι÷±Θ°
Θ®3Θ©ΔΌ»τΓςADP![]() ΓςBPQΘ§
ΓςBPQΘ§
‘ρAD=BPΘ§Θ§AP=BQΘ§
‘ρ![]() Θ§
Θ§
ΫβΒΟ![]() ΘΜ
ΘΜ
ΔΎ»τΓςADP![]() ΓςBQPΘ§
ΓςBQPΘ§
‘ρAD=BQΘ§AP=BPΘ§
‘ρ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘΚ¥φ‘Ύ![]() Μρ
Μρ![]() Θ§ ΙΒΟΓςADP”κΓςBPQ»ΪΒ»Θ°
Θ§ ΙΒΟΓςADP”κΓςBPQ»ΪΒ»Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
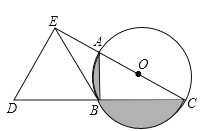
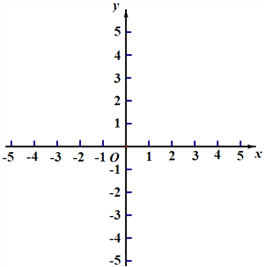
ΓΨΧβΡΩΓΩ»γΆΦΘ§ACΈΣΓ―OΒΡ÷±ΨΕΘ§BΈΣΓ―O…œ“ΜΒψΘ§ΓœACB=30ΓψΘ§―”≥ΛCB÷ΝΒψDΘ§ ΙΒΟCB=BDΘ§ΙΐΒψDΉςDEΓΆACΘ§¥ΙΉψE‘ΎCAΒΡ―”≥ΛœΏ…œΘ§Ν§Ϋ”BEΘ°
Θ®1Θ©«σ÷ΛΘΚBE «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©Β±BE=3 ±Θ§«σΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Εΰ¥ΈΚ· ΐ
÷–Θ§Εΰ¥ΈΚ· ΐ![]() ΒΡΕ‘≥Τ÷αΈΣ
ΒΡΕ‘≥Τ÷αΈΣ![]() Θ°Βψ
Θ°Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œ.
…œ.
Θ®1Θ©«σ![]() Θ§
Θ§ ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©»τΒψ![]() ‘ΎΕΰ¥ΈΚ· ΐ
‘ΎΕΰ¥ΈΚ· ΐ![]() …œΘ§«σ
…œΘ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©Β±Εΰ¥ΈΚ· ΐ![]() ”κ÷±œΏ
”κ÷±œΏ![]() œύΫΜ”ΎΝΫΒψ ±Θ§…ηΉσ≤ύΒΡΫΜΒψΈΣ
œύΫΜ”ΎΝΫΒψ ±Θ§…ηΉσ≤ύΒΡΫΜΒψΈΣ![]() Θ§»τ
Θ§»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
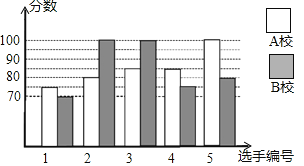
ΓΨΧβΡΩΓΩΡ≥ –ΨΌ––÷Σ Ε¥σ»ϋΘ§A–ΘΓΔB–ΘΗς≈…≥ω5Οϊ―Γ ÷Ήι≥…¥ζ±μΕ”≤ΈΦ”Ψω»ϋΘ§ΝΫ–Θ≈…≥ω―Γ ÷ΒΡΨω»ϋ≥…Φ®»γΆΦΥυ ΨΘ°
![]() ΗυΨίΆΦ ΨΧν–¥œ¬±μΘΚ
ΗυΨίΆΦ ΨΧν–¥œ¬±μΘΚ
ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ | |
A–Θ | ______ | 85 | ______ |
B–Θ | 85 | ______ | 100 |
![]() ΫαΚœΝΫ–Θ≥…Φ®ΒΡΤΫΨυ ΐΚΆ÷–ΈΜ ΐΘ§Ζ÷ΈωΡΡΗω―ß–ΘΒΡΨω»ϋ≥…Φ®ΫœΚΟΘΜ
ΫαΚœΝΫ–Θ≥…Φ®ΒΡΤΫΨυ ΐΚΆ÷–ΈΜ ΐΘ§Ζ÷ΈωΡΡΗω―ß–ΘΒΡΨω»ϋ≥…Φ®ΫœΚΟΘΜ
![]() ΦΤΥψΝΫ–ΘΨω»ϋ≥…Φ®ΒΡΖΫ≤νΘ§≤Δ≈–ΕœΡΡΗω―ß–Θ¥ζ±μΕ”―Γ ÷≥…Φ®ΫœΈΣΈ»Ε®Θ°
ΦΤΥψΝΫ–ΘΨω»ϋ≥…Φ®ΒΡΖΫ≤νΘ§≤Δ≈–ΕœΡΡΗω―ß–Θ¥ζ±μΕ”―Γ ÷≥…Φ®ΫœΈΣΈ»Ε®Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
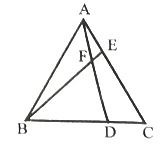
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψDΓΔEΖ÷±π‘ΎBCΓΔAC±Ώ…œΘ§«“
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψDΓΔEΖ÷±π‘ΎBCΓΔAC±Ώ…œΘ§«“![]() Θ§
Θ§![]() ”κ
”κ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ°
Θ°
Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ![]() ΒΡΕ» ΐΘ°
ΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
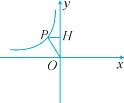
ΓΨΧβΡΩΓΩ»γΆΦ «Ζ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσΒΡ“Μ÷ßΘ°
ΒΡΆΦœσΒΡ“Μ÷ßΘ°
(1)«σmΒΡ»Γ÷ΒΖΕΈßΘ§≤Δ‘ΎΆΦ÷–Μ≠≥ωΝμ“Μ÷ßΒΡΆΦœσΘΜ
(2)»τmΘΫΘ≠1Θ§P(aΘ§3) «ΥΪ«ζœΏ…œΒΡ“ΜΒψΘ§PHΓΆy÷α”ΎHΘ§ΫΪœΏΕΈOPœρ”“ΤΫ“Τ3PHΒΡ≥ΛΕ»÷ΝOΓδPΓδΘ§¥Υ ±PΒΡΕ‘”ΠΒψPΓδ«ΓΚΟ‘ΎΝμ“ΜΧθΥΪ«ζœΏy=![]() ΒΡΆΦœσ…œΘ§‘ρΤΫ“Τ÷–œΏΕΈOP…®ΙΐΒΡΟφΜΐΈΣ Θ§k= .
ΒΡΆΦœσ…œΘ§‘ρΤΫ“Τ÷–œΏΕΈOP…®ΙΐΒΡΟφΜΐΈΣ Θ§k= .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
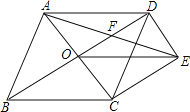
ΓΨΧβΡΩΓΩ»γΆΦΘ§Νβ–ΈABCDΒΡΕ‘Ϋ«œΏACΓΔBDœύΫΜ”ΎΒψOΘ§ΙΐΒψDΉςDEΓΈACΘ§«“DEΘΫ![]() ACΘ§Ν§Ϋ”CEΓΔOEΘ§Ν§Ϋ”AEΫΜOD”ΎΒψFΘ°
ACΘ§Ν§Ϋ”CEΓΔOEΘ§Ν§Ϋ”AEΫΜOD”ΎΒψFΘ°
Θ®1Θ©«σ÷ΛΘΚOEΘΫCDΘΜ
Θ®2Θ©»τΝβ–ΈABCDΒΡ±Ώ≥ΛΈΣ8Θ§ΓœABCΘΫ60ΓψΘ§«σAEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΖ¥±»άΐΚ· ΐyΘΫ©¹![]() Θ§œ¬Ν–Ϋα¬έΘΚΔΌΆΦœσ±ΊΨ≠ΙΐΒψΘ®©¹3Θ§1Θ©ΘΜΔΎΆΦœσ‘ΎΒΎΕΰΘ§ΥΡœσœόΡΎΘΜΔέyΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜΔήΒ±xΘΨ©¹1 ±Θ§yΘΨ3Θ°Τδ÷–¥μΈσΒΡΫα¬έ”–Θ®ΓΓΓΓΘ©
Θ§œ¬Ν–Ϋα¬έΘΚΔΌΆΦœσ±ΊΨ≠ΙΐΒψΘ®©¹3Θ§1Θ©ΘΜΔΎΆΦœσ‘ΎΒΎΕΰΘ§ΥΡœσœόΡΎΘΜΔέyΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜΔήΒ±xΘΨ©¹1 ±Θ§yΘΨ3Θ°Τδ÷–¥μΈσΒΡΫα¬έ”–Θ®ΓΓΓΓΘ©
A. ΔΌΔή B. ΔΎΔέ C. ΔΎΔή D. ΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψ![]() Θ§
Θ§![]() Θ§ΒψC «÷±œΏAB…œ“λ”ΎΒψBΒΡ»Έ“ΜΒψΘ§œ÷“‘BCΈΣ“Μ±Ώ‘ΎAB”“≤ύΉς’ΐΖΫ–ΈBCDEΘ§…δœΏOC”κ÷±œΏDEΫΜ”ΎΒψPΘ§»τΒψCΒΡΚαΉχ±ξΈΣmΘ°
Θ§ΒψC «÷±œΏAB…œ“λ”ΎΒψBΒΡ»Έ“ΜΒψΘ§œ÷“‘BCΈΣ“Μ±Ώ‘ΎAB”“≤ύΉς’ΐΖΫ–ΈBCDEΘ§…δœΏOC”κ÷±œΏDEΫΜ”ΎΒψPΘ§»τΒψCΒΡΚαΉχ±ξΈΣmΘ°

![]() «σ÷±œΏABΒΡΚ· ΐ±μ¥ο ΫΘ°
«σ÷±œΏABΒΡΚ· ΐ±μ¥ο ΫΘ°
![]() »τΒψC‘ΎΒΎ“ΜœσœόΘ§«“ΒψCΈΣOPΒΡ÷–ΒψΘ§«σmΒΡ÷ΒΘ°
»τΒψC‘ΎΒΎ“ΜœσœόΘ§«“ΒψCΈΣOPΒΡ÷–ΒψΘ§«σmΒΡ÷ΒΘ°
![]() »τΒψCΈΣOPΒΡ»ΐΒ»Ζ÷Βψ
»τΒψCΈΣOPΒΡ»ΐΒ»Ζ÷Βψ![]() Φ¥ΒψCΖ÷OP≥…1ΘΚ2ΒΡΝΫΧθœΏΕΈ
Φ¥ΒψCΖ÷OP≥…1ΘΚ2ΒΡΝΫΧθœΏΕΈ![]() Θ§«κ÷±Ϋ”–¥≥ωΒψCΒΡΉχ±ξΘ°
Θ§«κ÷±Ϋ”–¥≥ωΒψCΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com