
 如图,AB-BC-CD是一根三节棍,其中线段AB、BC、CD首尾顺次相连,且AB=BC=CD,将这个三节棍摆放在△AMD中,使它的两个端点与△AMD两个顶点重合,三节棍的首尾两节在△AMD的边上,则AB-BC-CD就是△AMD的配套三节棍.
如图,AB-BC-CD是一根三节棍,其中线段AB、BC、CD首尾顺次相连,且AB=BC=CD,将这个三节棍摆放在△AMD中,使它的两个端点与△AMD两个顶点重合,三节棍的首尾两节在△AMD的边上,则AB-BC-CD就是△AMD的配套三节棍.分析 (1)根据已知条件即可得到结论;
(2)根据等腰三角形的性质得到∠M=∠D,∠A=∠BCA,由平行线的性质得到∠BCA=∠D,等量代换得到∠A=∠D=∠M,于是得到结论.
解答  解:(1)∵∠A=60°,AB=BC,AB=BC=CA,
解:(1)∵∠A=60°,AB=BC,AB=BC=CA,
∵AD=60,
∴AB=BC=CA=CD=30,
∴△AMD的配套三节棍的总长为3×30=90;
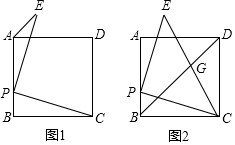
(2)①作射线AE,在射线AE上截取AB=BM,
②分别以A,M为圆心,AM的长为半径画弧,两弧交于点D,
③连接AD,MD,
④过B作BC∥DM交AD于D,
则图形即为所求;
证明:∵AM=AD,
∴∠M=∠D,
∵AB=BC,
∴∠A=∠BCA,
∵BC∥MD,
∴∠BCA=∠D,
∴∠A=∠D=∠M,
∵∠A+∠D+∠M=180°,
∴∠A=60°,
点评 本题考查了作图-应用与设计作图,平行线的性质,等边三角形的性质,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.
如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
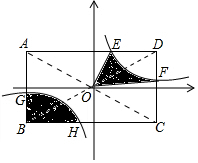 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与对角线交点在原点的矩形ABCD交于点E,F,G,H且E(1,3),AB:BC=$\frac{1}{2}$,图中阴影部分的面积为15.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与对角线交点在原点的矩形ABCD交于点E,F,G,H且E(1,3),AB:BC=$\frac{1}{2}$,图中阴影部分的面积为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com