为了发展教育事业,政府不断加大了对教育事业的投入,据统计某市初中生均教育事业费的投入从2008年的6000元增加到2010年的7260元.
(1)求该市2008年至2010年初中生均教育事业费投入的年平均增长率是多少?
(2)如果该市今后几年初中生均教育事业费的投入按此增长率增长,预测2012年该市初中生均教育事业费的投入为多少元?
解:(1)设该市2008年至2010年初中生均教育事业费投入的年平均增长率是x,
根据题意得:6000(1+x)
2=7260,
化简得:(1+x)
2=

,
即1+x=
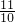
,或1+x=-
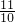
,
解得:x
1=0.1=10%,x
2=-2.1(舍去).
答:该市2008年至2010年初中生均教育事业费投入的年平均增长率是10%.
(2)7260(1+10%)
2=8784.6(元).
答:2012年该市初中生均教育事业费的投入为8784.6元.
分析:本题为增长率问题,一般用增长后的量=增长前的量×(1+增长率)来解决问题,
(1)设该市2008年至2010年初中生均教育事业费投入的年平均增长率是x,则2009年的产值是6000(1+x),2010年的产值是6000(1+x)
2,而题中又已知2010年教育事业的投入费用达到7260元,进而建立等量关系列出方程求解;
(2)利用(1)得到的增长率,根据2011年是在2010年的基础上增长,用2010的教育事业投入的钱数×(1+增长率)即为2011年教育事业投入的钱数:7260×(1+10%),而2012年的钱数又是在2011年基础上增长的,所以用2011的教育事业投入的钱数×(1+增长率)即为2012年教育事业投入的钱数:7260(1+10%)
2,计算出结果即可.
点评:本题考查了一元二次方程的应用,可按照增长率的一般规律进行解答.列方程解应用题的关键是找出题中的等量关系,用到的基本的等量关系是:增长后的量=增长前的量×(1+增长率),要求学生必须搞清关系式中增长前的量和增长后的量在原题中所代表的值.实际应用问题一定要注意所求出的值是否都满足题意,需要进行合理的取舍.

 ,
,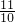 ,或1+x=-
,或1+x=-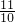 ,
,

 阅读快车系列答案
阅读快车系列答案