
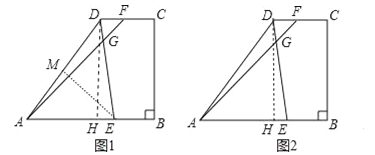
【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.

【答案】(1)7;(2)15或![]() ;(3)
;(3)![]() (
(![]() ).
).
【解析】
试题分析:(1)作DH⊥AB于H,如图1,易得四边形BCDH为矩形,则DH=BC=12,CD=BH,再利用勾股定理计算出AH,从而得到BH和CD的长;
(2)分类讨论:当EA=EG时,则∠AGE=∠GAE,则判断G点与D点重合,即ED=EA,作EM⊥AD于M,如图1,则AM=![]() AD=
AD=![]() ,通过证明Rt△AME∽Rt△AHD,利用相似比可计算出此时的AE长;当GA=GE时,则∠AGE=∠AEG,可证明AE=AD=15,(3)作DH⊥AB于H,如图2,则AH=9,HE=AE﹣AH=x﹣9,先利用勾股定理表示出DE=
,通过证明Rt△AME∽Rt△AHD,利用相似比可计算出此时的AE长;当GA=GE时,则∠AGE=∠AEG,可证明AE=AD=15,(3)作DH⊥AB于H,如图2,则AH=9,HE=AE﹣AH=x﹣9,先利用勾股定理表示出DE=![]() ,再证明△EAG∽△EDA,则利用相似比可表示出EG=
,再证明△EAG∽△EDA,则利用相似比可表示出EG=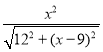 ,则可表示出DG,然后证明△DGF∽△EGA,于是利用相似比可表示出x和y的关系.
,则可表示出DG,然后证明△DGF∽△EGA,于是利用相似比可表示出x和y的关系.
试题解析:(1)作DH⊥AB于H,如图1,易得四边形BCDH为矩形,∴DH=BC=12,CD=BH,在Rt△ADH中,AH=![]() =
=![]() =9,∴BH=AB﹣AH=16﹣9=7,∴CD=7;
=9,∴BH=AB﹣AH=16﹣9=7,∴CD=7;
(2)当EA=EG时,则∠AGE=∠GAE,∵∠AGE=∠DAB,∴∠GAE=∠DAB,∴G点与D点重合,即ED=EA,作EM⊥AD于M,如图1,则AM=![]() AD=
AD=![]() ,∵∠MAE=∠HAD,∴Rt△AME∽Rt△AHD,∴AE:AD=AM:AH,即AE:15=
,∵∠MAE=∠HAD,∴Rt△AME∽Rt△AHD,∴AE:AD=AM:AH,即AE:15=![]() :9,解得AE=
:9,解得AE=![]() ;
;
当GA=GE时,则∠AGE=∠AEG,∵∠AGE=∠DAB,而∠AGE=∠ADG+∠DAG,∠DAB=∠GAE+∠DAG,∴∠GAE=∠ADG,∴∠AEG=∠ADG,∴AE=AD=15,综上所述,△AEC是以EG为腰的等腰三角形时,线段AE的长为![]() 或15;
或15;
(3)作DH⊥AB于H,如图2,则AH=9,HE=AE﹣AH=x﹣9,在Rt△ADE中,DE=![]() =
=![]() ,∵∠AGE=∠DAB,∠AEG=∠DEA,∴△EAG∽△EDA,∴EG:AE=AE:ED,即EG:x=x:
,∵∠AGE=∠DAB,∠AEG=∠DEA,∴△EAG∽△EDA,∴EG:AE=AE:ED,即EG:x=x:![]() ,∴EG=
,∴EG=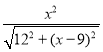 ,∴DG=DE﹣EG=
,∴DG=DE﹣EG=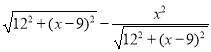 ,∵DF∥AE,∴△DGF∽△EGA,∴DF:AE=DG:EG,即y:x=(
,∵DF∥AE,∴△DGF∽△EGA,∴DF:AE=DG:EG,即y:x=(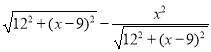 ):
):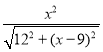 ,∴
,∴![]() (9<x<
(9<x<![]() ).
).


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】由二次函数y=2(x﹣3)2+1,可知( )
A.其图象的开口向下
B.其图象的对称轴为直线x=﹣3
C.其最小值为1
D.当x<3时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5个红球、4个白球放入一个不透明的盒子里,从中摸出6个球,恰好红球与白球都摸到,这个事件( )
A. 不可能发生B. 可能发生C. 很可能发生D. 必然发生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).
(1)判断直线![]() 与正方形OABC是否有交点,并求交点坐标。
与正方形OABC是否有交点,并求交点坐标。
(2)将直线![]() 进行平移,平移后恰好能把正方形OABC分为面积相等的两部分,请求出平移后的直线解析式.
进行平移,平移后恰好能把正方形OABC分为面积相等的两部分,请求出平移后的直线解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个同学分别解一道一元二次方程x2+bx+c=0,甲因把一次项系数看错了,而解得方程两根为-3和5,乙把常数项看错了,解得两根为2和2,则原方程是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com