
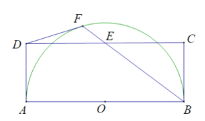
【题目】如图,在矩形ABCD中,边AB是半圆O的直径,点E是CD的中点,BE交半圆O于点F,连接DF.
(1)求证:DF是半圆O的切线;
(2)若AB =8,AD =3,求BF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OF、OD、AF,根据矩形的性质和已知条件可得DE=![]() CD,OB=
CD,OB=![]() AB,DC∥AB,∠OAD=90°,然后利用SAS证出△AOD≌△FOD,即可证出∠OAD=∠OFD=90°,然后根据切线的判定定理即可证出结论;
AB,DC∥AB,∠OAD=90°,然后利用SAS证出△AOD≌△FOD,即可证出∠OAD=∠OFD=90°,然后根据切线的判定定理即可证出结论;
(2)根据相似三角形的判定证出Rt△AOD∽Rt△FBA,然后列出比例式,根据比例式设AF=3x,BF=4x,然后根据勾股定理列出方程即可求出结论.
(1)证明:连接OF、OD、AF,

在矩形ABCD中,
∵点E是CD的中点,点O是AB的中点,
∴DE=![]() CD,OB=
CD,OB=![]() AB,DC∥AB,∠OAD=90°
AB,DC∥AB,∠OAD=90°
∴四边形OBED为平行四边形
∴OD∥BF
∴∠AOD=∠OBF,∠OFB=∠FOD
∵OB=OF
∴∠OBF=∠OFB
∴∠AOD=∠FOD,
∵OA=OF,OD=OD
∴△AOD≌△FOD(SAS)
∴∠OAD=∠OFD=90°,
∴OF⊥DF,即DF为半圆O的切线
(2)由(1)知:在Rt△AOD和Rt△FBA中,
∠AOD=∠OBF,∠DAO=∠BFA=90°
∴Rt△AOD∽Rt△FBA
∴![]()
又在矩形ABCD中,AB=8,AD=3,则OA=4,
∴![]()
∴可设AF=3x,BF=4x
在Rt△ABF中,AB2=AF2+BF2
82=(3x)2+(4x)2
解得,x1=![]() ,x2=-
,x2=-![]() (舍)
(舍)
即BF=![]()


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 直径,
直径,![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() ,连
,连![]() 接交
接交![]() 于点
于点![]()
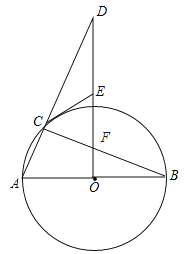
(1)求证:![]()
(2)连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,填空:
,填空:
①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为菱形;
为菱形;
②当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 为正方形;
为正方形;
查看答案和解析>>
科目:初中数学 来源: 题型:
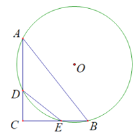
【题目】如图,在△ABC中,tan∠BAC![]() tan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
tan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
A.![]() B.
B.![]()
C.13D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
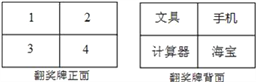
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
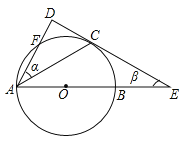
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
![]() 连接
连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com