
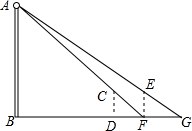
 如图,河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.7m,求路灯杆AB的高度.
如图,河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.7m,求路灯杆AB的高度. 分析 根据相似三角形的判定与性质分别得出比例式,进而利用BD,AB的长.
解答 解:∵AB∥CD,
∴△ABF∽△CDF,
∴$\frac{AB}{CD}$=$\frac{BF}{DF}$,
即$\frac{AB}{1.7}$=$\frac{3+DB}{3}$,
∵AB∥EF,
∴△ABG∽△EFG,
∴$\frac{AB}{EF}$=$\frac{BG}{FG}$,
即$\frac{AB}{1.7}$=$\frac{BD+7}{4}$,
∵CD=EF,
∴$\frac{3+BD}{3}$=$\frac{7+BD}{4}$,
解得:BD=9(m),
把BD=9代入$\frac{AB}{1.7}$=$\frac{3+9}{3}$,
解得:AB=6.8m,
答:路灯AB的高度为6.8m.
点评 此题主要考查了相似三角形的应用,正确得出BD的长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a,b,c | B. | b,c,d | C. | a,c,d | D. | a,b,d |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 政府决定实施“煤改气”供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
政府决定实施“煤改气”供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com