
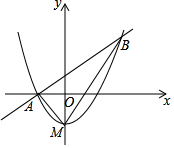
 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.分析 (1)由条件可分别求得A、B的坐标,设出抛物线解析式,利用待定系数法可求得抛物线解析式;
(2)结合(1)中A、B、C的坐标,根据勾股定理可分别求得AB、AM、BM,可得到AB2+AM2=BM2,可判定△ABM为直角三角形.
解答 解:(1)∵A点为直线y=x+1与x轴的交点,
∴A(-1,0),
又B点横坐标为2,代入y=x+1可求得y=3,
∴B(2,3),
∵抛物线顶点在y轴上,
∴可设抛物线解析式为y=ax2+c,
把A、B两点坐标代入可得$\left\{\begin{array}{l}{a+c=0}\\{4a+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{c=-1}\end{array}\right.$,
∴抛物线解析式为y=x2-1;
(2)△ABM为直角三角形.理由如下:
由(1)抛物线解析式为y=x2-1,可知M点坐标为(0,-1),
∴AM2=12+12=2,AB2=(2+1)2+32=18,BM2=22+(3+1)2=20,
∴AM2+AB2=2+18=20=BM2,
∴△ABM为直角三角形.
点评 本题考查了待定系数法求二次函数的解析式,二次函数的性质,勾股定理及其逆定理等知识点.在(1)中确定出A、B两点的坐标是解题的关键,在(2)中分别求得AB、AM、BM的长是解题的关键.本题考查知识点较为基础,难度适中.


科目:初中数学 来源: 题型:选择题
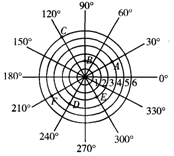 如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )| A. | A(4,30°) | B. | B(2,90°) | C. | C(6,120°) | D. | D(3,240°) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 86×102 | B. | 8.6×103 | C. | 86×103 | D. | 0.86×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
| 发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
| 发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 ∠ACB=∠ADC=90°,AC=3,CD=2.当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似.
∠ACB=∠ADC=90°,AC=3,CD=2.当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com